Hay un número de funciones lógicas que son muy utilizados en circuitos digitales y, por tanto, puede encontrarse "listas" en las distintas familias de circuitos integrados. La reunión de estas funciones permite llevar a cabo proyectos capases de realizar operaciones más complejas. Los circuito integrados realizan las operaciones más simples.
Este artículo puede considerarse una continuación de otros dos (ART284S y ART283) en la que nos ocupamos de conceptos fundamentales de la electrónica digital.
Analicemos las principales funciones:
a) La función E
La función E o AND (inglés) corresponde a multiplicación binaria y se representa por el símbolo en la figura 1.
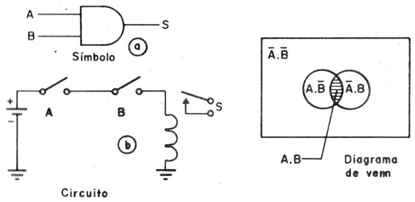
El circuito equivalente para el relé y llaves es mostrado en (b) y en la misma figura, tenemos la representación de un diagrama de Ven.
Este diagrama tiene el universo Ã.B, y dentro de este universo, las posibilidades de valores asumidos por A y B. Entonces tenemos la región en que A es presente, pero B no (/B = negativa de B) y la región común que corresponde al universo en el que la salida es 1, es decir, A.B.
La región rayada corresponde a la intersección de clases, donde A y B deben considerarse simultáneamente.
El uso de este tipo de diagrama, que no será visto en profundidad aquí, es muy útil en la preparación de proyectos que utilizan funciones lógicas.
La tabla verdad para la función E es:

Podemos expresar la función con el uso de una frase que permite fácilmente la memorización:
"La salida será en el nivel Hl se y sólo se, las entradas A y B al mismo tiempo, están en el nivel Hl."
También podemos tener una función E de tres entradas, o una "Puerta E” de tres entradas, como se muestra en la figura 2.
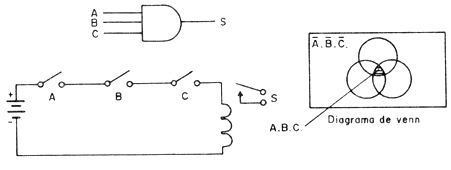
En la misma figura se muestra el circuito equivalente con tres llaves y un relé. Como podemos ver, el relé sólo estar energizado si A, B y C están cerradas al mismo tiempo.
La tabla de verdad para tres entradas y esta función será:

Para cualquier situación que no sea de las tres entradas en nivel 1 o HI la salida es cero o LO.
Tenga en cuenta que contamos con 8 diferentes combinaciones de entrada, de las cuales sólo 1 resulta en la señal en el nivel Hl. Otra representación para la función E se muestra en la figura 3.
También tenga en cuenta lector que usamos la palabra " puerta” (del Inglés Gate) para representar un circuito que ejecuta una combinación lógica. Por lo tanto, decir "puerta E" es como decir “circuito que ejerce la función E".
b) La función OU
La función de O o OR (del inglés) corresponde la adición binaria, es representada por el símbolo en la figura 4.
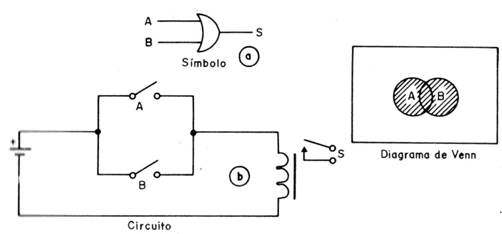
El circuito equivalente se muestra en (b) de la misma figura que consta de 2 llaves conectadas en paralelo, que puede energizar un relé.
Como podemos ver, el relé se energiza si se activa una entrada O otra. Es decir, tenemos una salida de nivel HI si A o B son activadoas o tomado al nivel 1.
El diagrama de Venn para esta función se da en la misma figura.
Vea que la salida del universo 1 es mayor que en la función, debido a que la región sombreada cubre tanto a como B.
Podemos escribir esta función:
S = A + B
La tabla de verdad para esta función es la siguiente:
| A | B | (A + B) = salida | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
También podemos tener una función O de tres entradas que se pueden representar como se muestra en la figura 5.
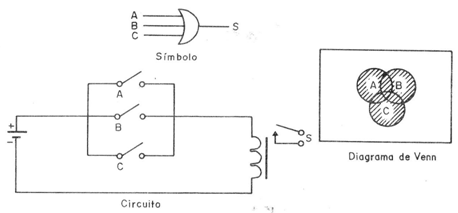
La tabla de verdad para esta función será entonces:
| A | B | C | (A+B+C) = salida |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
Tenga en cuenta que para la salida 1 una o más entradas deben estar a 1 o nivel alto. Para tres entradas también son 8 combinaciones las podemos obtener, es las que una sola salida es LO.
c) La Función NO E o NE.
La función NO E o NOR (del inglés) que corresponde a la negación de E se representa como se muestra en la figura 6.
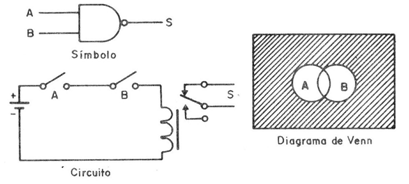
En la misma figura el diagrama de Venn que refleja claramente que este universo es precisamente lo que no está cubierto por la función E.
El circuito equivalente con relé muestra que utilizamos contactos NF en vez de NA en vez de al revés el resultado, que es equivalente a "apagado" en lugar de energizar con la acción de las teclas.
Lo mismo sería posible si, en la salida de la función E, conectarnos un circuito inversor con transistores u otros elementos.
Como el lector puede ver en la salida del símbolo adoptado se tiene una pequeña esfera que indica la negación.
Otro tipo de símbolo para esta función se muestra en la figura 7.
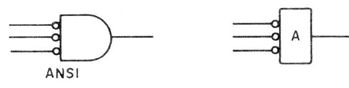
La tabla de verdad para la función será:

También, podemos tener una puerta NO E o NOR de tres entradas que serán representadas como se muestra en la figura 8.
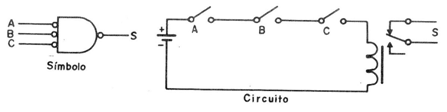
En la misma figura se muestra el circuito equivalente con tres llaves conectadas en paralelo, más el relé contactos NF usados.
La tabla de verdad para este circuito será:

La salida estará en el nivel HI cuando todas las entradas estén en el nivel LO.
d) La Función Inversora
La función NO o NOT es un simple inversor que ya hemos tenido la oportunidad de examinar cuando se habla de circuitos lógicos. Ella es también muy utilizada y puede ser representada como se muestra en la figura 9.
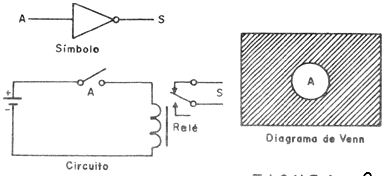
El diagrama de Venn para esta función se muestra en la misma figura, así como el circuito equivalente en la cual tenemos un relé con los contactos NF empleados.
La tabla de verdad para esta función es bastante simple, ya que sólo tenemos una entrada y una salida:
A -> Ã
0 -> 1
1 -> 0
Cuando la entrada está en el nivel HI la salida estará en LO y viceversa, así para la función NO.
e) Función NO-O o NO
La función NO O u NOU es la negación de la función O todavía, NOR del inglés.
La representación de esta función se muestra en la figura 10.
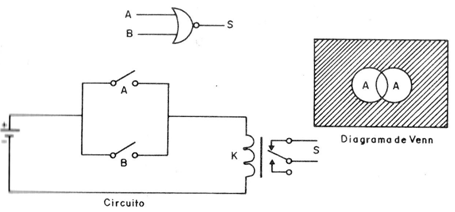
En la misma figura, así como el circuito equivalente utilizando un relé y dos llaves conectadas en paralelo, se muestra el diagrama de Venn. Observe el uso de los contactos NF del relé.
Otra representación para este puerto se muestra en la figura 11.
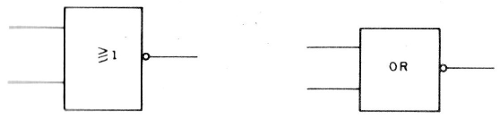
La tabla de verdad se expone a continuación:

También podemos tener esta puerta con tres entradas, que se muestra en la figura 12.
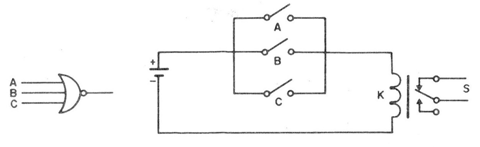
¡El circuito equivalente con los interruptores y relés se muestra en la figura misma, observando las obras símbolo! La presencia de la negación en la forma de la esfera en la salida.
La tabla de verdad para este caso será:
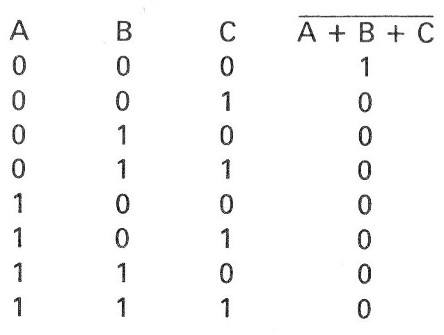
Vea que sólo tendremos la salida en el nivel HI cuando todas las entradas estén en el nivel LO.
f) Función O-exclusivo
La función O-exclusivo o Exclusive-OR es una de las más importantes en la electrónica digital y su símbolo se muestra en la figura 13.
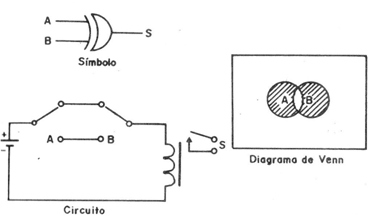
Vea que esta función es un poco diferente de O, ya que las teclas del circuito equivalente no son simples de interruptores, pero llaves de 1 polo X 2 posiciones.
La misma figura muestra el diagrama de Venn y la tabla de verdad es la siguiente:
Vea que tenemos la salida de 1 nivel con un desnudo otra entrada nivel Hl. Si las dos entradas estuvieran en el nivel LO o el nivel de Hl la salida será LO o 0.
Reuniendo estas funciones puede tener los circuitos lógicos más complejos, como veremos a continuación y en el futuro.




