Cuando los resistores están conectados en serie o paralelo de la manera convencional, es decir, siguiendo los patrones que fácilmente podemos percibir que se encuentran de ese modo, la aplicación de la fórmula es el único recurso necesario para obtener la resistencia equivalente.
Cuando, sin embargo, los resistores se conectan de manera un poco más disfrazados en que el técnico menos experimentado se siente difícil en saber cómo están conectados.
Para obtener la resistencia equivalente, la cosa se vuelve un poco más complicada lo que ocurre en el caso de una asociación que ya vimos en el sitio
Si bien aparentemente los resistores están conectados en serie, ya que aparecen "en fila" de la manera convencional, no es lo que ocurre en la realidad, dadas las conexiones externas. Para la resolución de esta prueba tenemos, por lo tanto, que usar un artificio que consiste para transformar este circuito en un equivalente en el que el modo de conexión se haga visible.
Para ello, damos nombres a los nodos, es decir, puntos de interconexiones. Así, el mismo circuito, puede ser transformado en el equivalente de la figura, que. fácilmente percibimos que se trata de una conexión en paralelo.
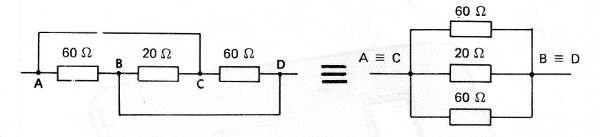
Así, como se trata de tres resistores en paralelo, tenemos que aplicar la fórmula tradicional:
1/R = 1/R1 + 1/R2 + 1/R3
1/R = 1/60 + 1//20 + 1/60
Extracción El mínimo múltiple común y reduciendo al mismo denominador tenemos:
1/R = (1 + 3 + 1) /60
1/R = 5/60
1/R = 1/12
Obtenemos de este modo 1 / R o sea, el inverso de R. Como, sin embargo, queremos obtener R, debemos invertir ese resultado de donde obtenemos:
que es la respuesta correcta a la cuestión propuesta.





