Cada parlante de un sistema de sonido reproduce correctamente una banda limitada de frecuencias. Para garantizar su perfecto funcionamiento es preciso separar las seriales del amplificador, que cubre toda la banda audible, de modo que, cada parlante reciba apenas la energía de las frecuencias con que puede trabajar. Para esta separación se utilizan filtros divisores de frecuencia, que constan de un conjunto de capacitores y bobinas dimensionados de acuerdo con las características de cada parlante usado y dela potencia del amplificador (como se explico en diferentes artículos este sitio). Proyectar estos filtros es de mucho interés para los lectores que trabajan con sonido, o que les gusta realizar sus propios diseños de cajas acústicas. Recordamos que en otros artículos se trato íntegramente la construcción de las cajas.
Obs. Este articulo es de 1991.
Los parlantes no pueden reproducir normalmente, y con la misma eficiencia, sonidos de toda la frecuencia de la banda audible. Esto se debe tanto a su formato como también al tamaño y a la propia dinámica del sistema que propulsiona el cono del mismo.
Por este motivo, se aprecia mejor desempeño en los sistemas de sonido en los que el fabricante posee lineas de parlantes que se destinan a bandas específicas.
Estrechando la banda de operación de un parlante podemos mejorar su desempeño y así obtener mayor fidelidad para nuestro sistema. Está claro que eso implica la utilización de mas de un parlante y también de dispositivos que puedan separar las señales de las diferentes bandas. Estos últimos se denominan filtros separadores de frecuencias o divisores de frecuencia.
En la figura 1 mostramos el espectro audible con la denominación de las diferentes bandas en las que los diversos tipos de parlantes pueden reproducir.
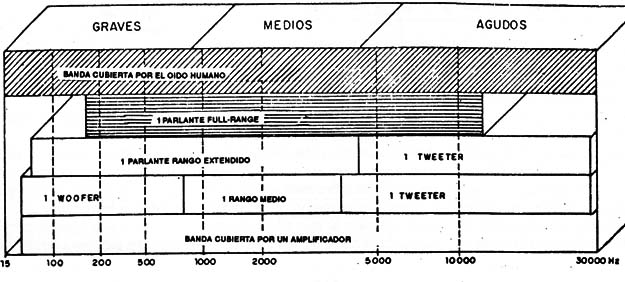
Para la reproducción de los agudos podemos tener un tweeter. Mientras que para la reproducción de los graves podemos usar un woofer, un rango extendido o también un full-range con menor rendimiento.
Las señales deben ser separadas antes de ser aplicadas a los parlantes, ya que si en un parlante destinado a la reproducción de agudos, le aplicamos también señales de medias y bajas frecuencias, además de no reproducirlas, la potencia del amplificador se disipará en forma de calor.
Esto puede ocasionar la destrucción de los parlantes y además sobrecargar los circuitos de salida del amplificador de potencia.
Por lo tanto es importante que cada parlante sólo reciba las señales que puede reproducir eficientemente. Para los parlantes más usados tenemos, entonces, las siguientes posibilidades de utilización
Full-range: este parlante se utiliza para reproducir de mejor manera toda la banda audible, aunque también posee sus limitaciones. Por eso es indicado para sistemas económicos, ya que si un solo parlante cubre toda la banda no es necesario un divisor de frecuencias.
Rango extendido: está destinado a los medios y graves, por lo tanto debe ser complementado con un tweeter. Este sistema de dos parlantes requiere, por lo tanto, un divisor de 2 vias o canales.
Woofer: son requeridos para la reproducción de bajas frecuencias (graves). Se complementa con un "medio”, un tweeter y un divisor de 3 vias.
Rango medio: cubren la banda de frecuencia media. Se complementa con un woofer un tweeter y un divisor de 3 vias.
Tweeter: se adoptan para las altas frecuencias (agudos) y se puede complementar con un rango extendido o con un woofer y un rango medio. Para el primer complemento se necesitará un divisor de 2 vias y para el segundo uno de 3.
Los Filtros
Según lo visto, los filtros divisores deben ser intercalados entre el amplificador y el parlante, para que cada uno reciba la senal apropiada a sus características.
Los filtros comunes, denominados pasivos, utilizan bobinas y capacitores para la separación de las diversas frecuencias.
Difieren de los filtros activos, ya que éstos utilizan transistores e integrados incorporados en los amplificadores.
Las bobinas y los capacitores presentan un componente "selectivo" en relación a la corriente alterna quele es aplicada, o sea, las corrientes que normalmente corresponde a los sonidos en las salidas de los amplificadores (figura 2).
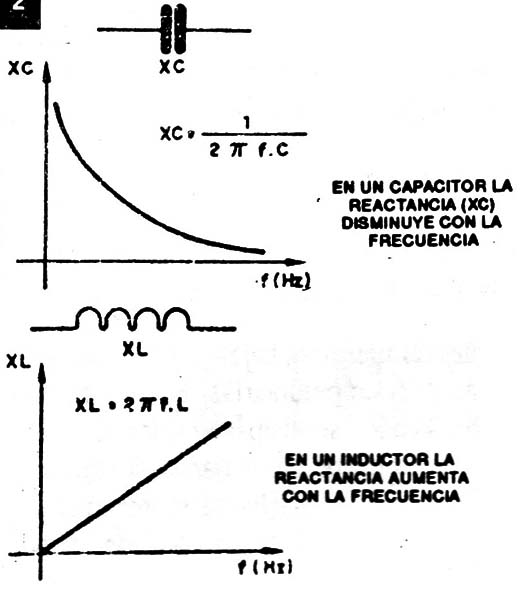
Los capacitores presentan una oposición menor a una señal cuanto mayor es su frecuencia. Mientras que los inductores presentan una oposición mayor a una señal cuanto mayor es su frecuencia.
Combinando estas características en circuitos que utilizan dos o mas de estos componentes podemos tomarlos selectivos, separando en dos o más vias las señales de diversas bandas de frecuencias.
El filtro más utilizado en la práctica es el de red de resistencias constante, que presenta la importante propiedad de mantener constante la impedancia del conjunto, en toda la banda de frecuencias que debe ser reproducida.
Para un amplificador, donde la potencia entregada para la reproducción depende de la impedancia del sistema reproductor, sólo tendremos el rendimiento ideal en toda la banda audible. En esta banda la impedancia se debe mantener en un valor fijo.
Su aumento, en una determinada porción del espectro, significa menor rendimiento de reproducción en esta banda.
Mientras que la disminución significa peligro de sobrecarga al circuito cuando las señales de esta banda fueran reproducidas.
Una característica importante que expresa el comportamiento de un filtro es la atenuación de cada sector del mismo. Esta atenuación se expresa en dB (decibeles) por octava. Su gráfico típico se muestra en la figura 3.
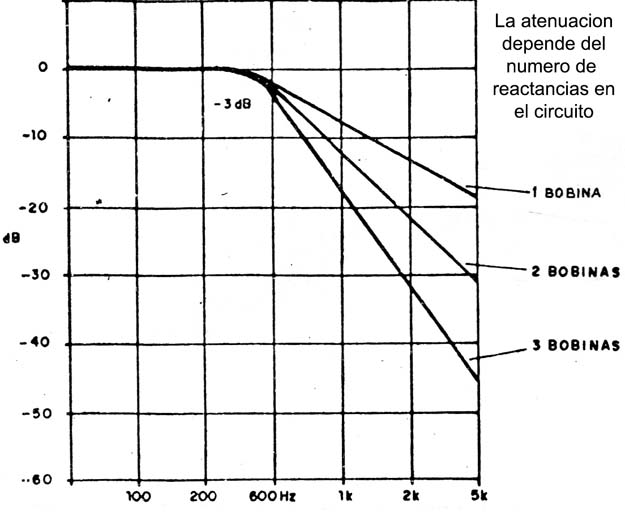
Allí se observa que la pendiente dela curva se acentúa más cuanto mayor es el número de bobinas utilizadas en el filtro.
Ahora, analizaremos el comportamiento de los filtros indicados en el gráfico: la inclinación de la curva para abajo indica la atenuación del filtro en dB por octava, o sea, a cuántos dB queda reducida la intensidad de la serial a partir del momento en que el filtro entra en acción (próximo a los 600Hz) hasta una frecuencia que corresponda a 1/8 del doble o más.
Por ejemplo. un filtro de 3dB por octava que actúe a partir de los 800Hz provoca una reducción de 3dB en la serial entre 800 y 1600Hz. La serial de 1600 pasará por este filtro con una intensidad aproximadamente dos veces menor que la de 800.
Los filtros comúnmente usados en cajas acústicas poseen atenuaciones en la banda de 6 a 12dB por octava.
Como la acción de los filtros es por bandas, podemos colocar todo eso en un gráfico único como muestra la figura 4.
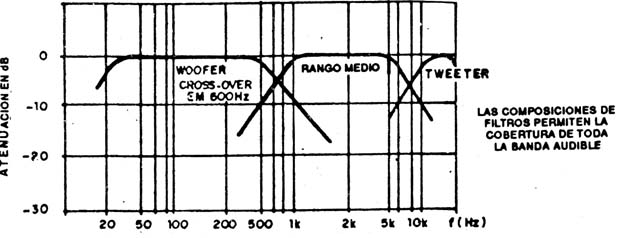
Observe, entonces, que existen puntos en que un filtro no deja pasar más las señales, al mismo tiempo que otro filtro comienza a permitir su paso y un punto de intersección o "cross over" que depende de las características de los parlantes empleados.
En el proyecto de un filtro se debe tener en cuenta diversos factores:
- Frecuencias o bandas de frecuencias que cada parlante debe reproducir.
- Potencia del amplificador.
- Impedancia que se desea para el conjunto.
- Eficiencia de separación de los canales (dB) por octava.
Para esto tenemos diversas posibilidades que serán, a partir de ahora. analizadas en circuitos prácticos y en procedimientos de cálculo.
Cálculos de circuitos prácticos
En la figura 5 mostramos circuitos del tipo serie/paralelo equivalentes que otorgan una atenuación de 6dB por octava operando en tres canales.
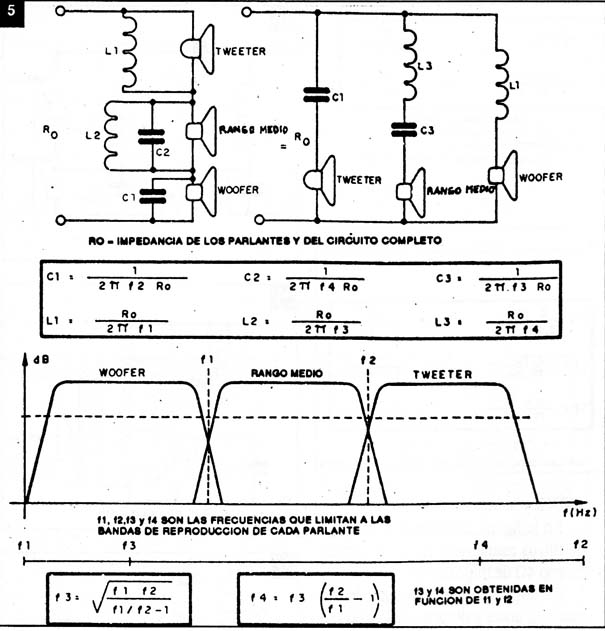
En la misma figura tenemos las fórmulas que permiten calcular los componentes y la operaciones. En estas fórmulas las capacidades son expresadas en Farad (F), las inductancias en Henry (H) y las frecuencias en Hertz (Hz). Ro es la impedancia del circuito y está dada en Ohm.
Observe que una vez que la salida del amplificador sea de 4 Ohm, entonces, Ro como todas las impedancias de los parlantes usados deben tener ese mismo valor. No debemos "mezclar" parlantes de impedancias diferentes en un sistema. En la figura 6 tenemos un filtro de 12dB por octava para tres parlantes con la fórmula para los cálculos de sus diversos componentes.
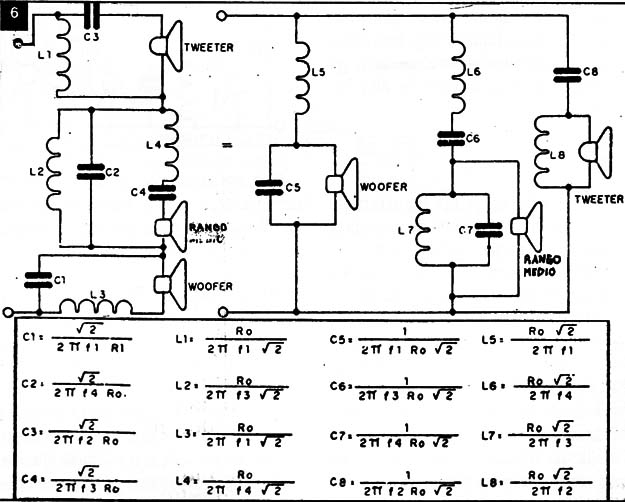
Inductancias, capacidades, frecuencias e impedancias son expresadas en las unidades antes mencionadas. Las dos configuraciones. serie y paralelo, son equivalentes también en este caso.
Para dos parlantes, un filtro que usa un woofer o un rango extendido y un tweeter tenemos el diagrama y las fórmulas en la figura 7.
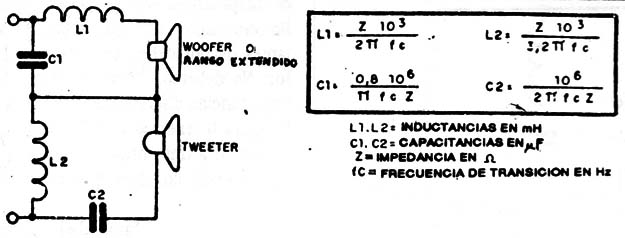
Este filtro tiene una atenuación de 12dB por octava y las unidades son las mismas de los proyectos anteriores.
Para una atenuación de 18dB por octava, con dos parlantes tenemos el interesante filtro en ? de la figura 8.
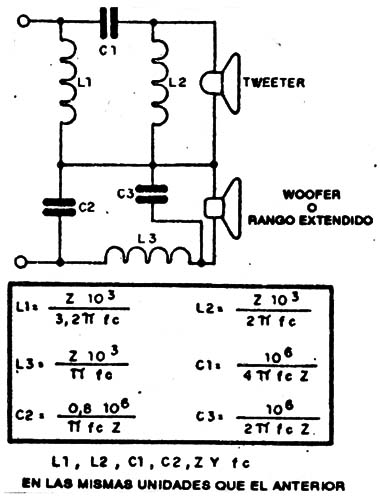
Se usan tres bobinas y tres capacitores y las fórmulas son las dadas en la misma figura. En estas fórmulas, z es la impedancia de los parlantes y de la salida del amplificador expresadas en Ohm.
Ejemplos prácticos
Aclaramos que si el lector parte de parlantes convencionales, con características dentro de bandas normales, los cálculos no son necesarios, adoptándose entonces uno de los circuitos prácticos que damos a continuación.
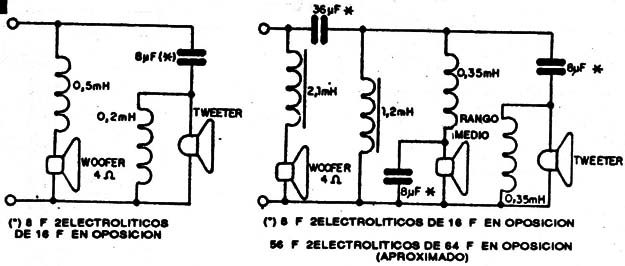
Tenemos entonces un circuito simple con 6dB por octava con tres parlantes para una impedancia de 8 Ω (figura 9).
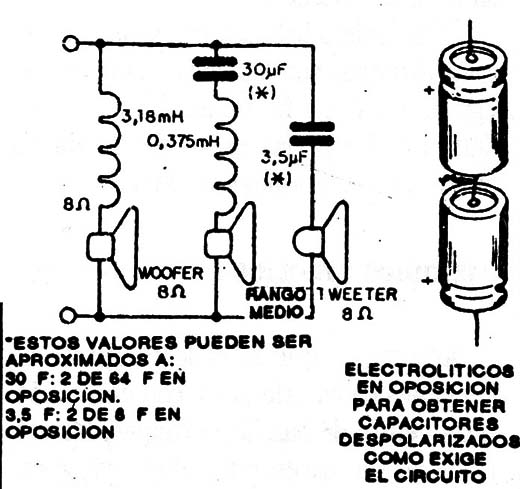
Observe que, como no siempre es posible encontrar capacitores despolarizados para este tipo de aplicaciones, el uso de electrolíticos exige algunos cuidados; debemos unir dos capacitores en oposición, conforme a la figura 9 para que su operación pueda ser hecha con señales de audio.
De esta manera los valores se alterarán (por ejemplo: para obtener 30uF aproximadamente; se debe conectar dos capacitores de 64uF en oposición).
En la figura 10 tenemos un circuito de tres canales con atenuación de 12dB por octava con impedancia de parlante de 8 Ω.
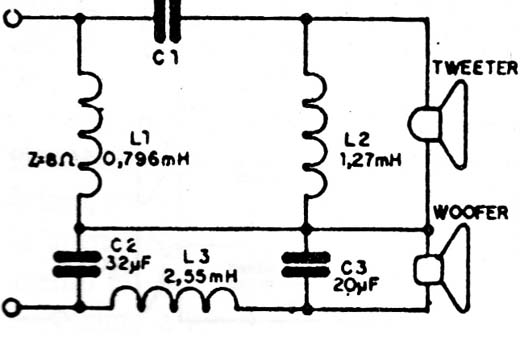
Las frecuencias de transición (cross-over) de este filtro se ubican en 500 y 4500Hz. Estos dos últimos circuitos fueron sugeridos por "Building Hi-Fi Speakers Systems" editado por Philips.
Para los canales con atenuación tenemos una frecuencia de transición de 1000Hz y una impedancia de 8 Ω.
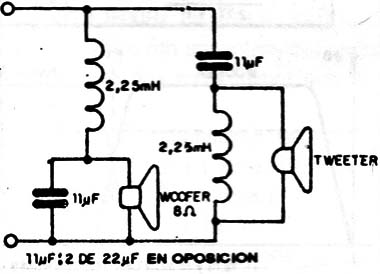
Para una atenuación mayor en los puntos de cross-over sugerimos, para dos canales, el filtro de la figura 12. La frecuencia de transición es también de 1000Hz y la impedancia de 8 Ω.
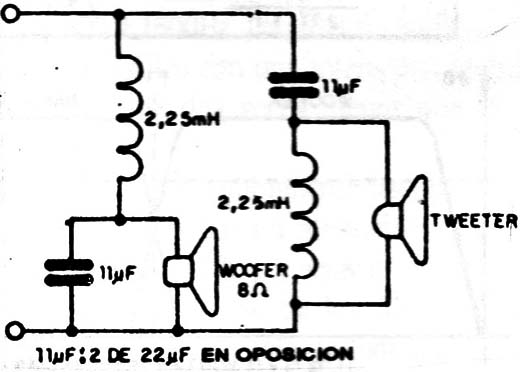
En la figura 13 vemos dos circuitos de filtros asimétricos para 2 o 3 canales con 4 Ω de impedancia.
En estos circuitos las curvas de atenuación, antes y después de la frecuencia de transición, no son iguales debido al hecho de que los componentes que forman la rama de baja frecuencia no ocupan posición equivalente a los componentes de la rama de alta frecuencia.
Bobinas
Los valores de las inductancias usadas en los divisores de frecuencia varían en una amplia banda y como normalmente las potencias de operación son elevadas, lo que significa circulación de contentes intensas, la obtención de estos componentes con valores exactos es muy difícil, tanto en lo que se refiere a la inductancia como al espesor del alambre.
Por lo tanto recomendamos que las bobinas sean realizadas por el propio lector.
Enrollar las bobinas es simple, lo complicado son los cálculos para la determinación de las espiras del alambre (esmaltado) en determinada forma para llegar a la inductancia necesaria.
Con aproximación podemos partir inicialmente, con el espesor del alambre para la banda de potencias más comunes, conforme ala siguiente tabla.
| ALAMBRE (AWG) | POTENCIAS |
| 22 hasta | 10W |
| 20 | 10 a 25W |
| 18 | 25 a 50W |
Se observa, que cuanto mayor es el número AWG del alambre, o sea, menor su espesor, mayor será la resistencia ôhmica que la bobina presentará y ésta es una característica indeseable en los filtros ya que ésta será responsable de perdidas de potencia.
Por ésto es recomendable que el alambre sea medianamente grueso.
Generalmente, se considera satisfactorio para una aplicación en audio, una bobina que tenga una resistencia ôhmica inferior a 1 ohm.
En la figura 14, vemos las dimensiones de la bobina que deben ser consideradas en el cálculo del número de espiras, y en la misma figura se encuentra la fórmula para el cálculo.
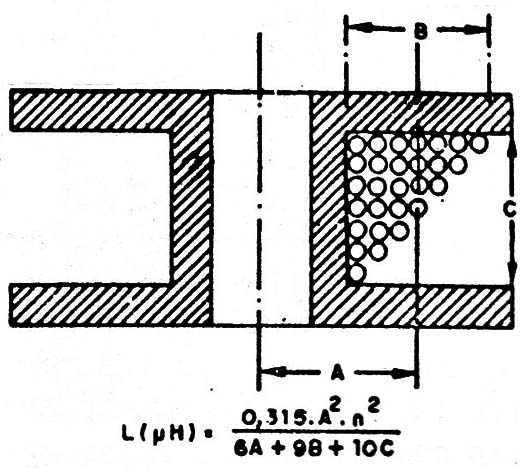
En esta fórmula n es el número de espiras, l es el valor de la inductancia en microhenry (uH) y A, B y C son las dimensiones de la bobina en centímetros.
Para que la fórmula se aproxime al máximo del valor real, las dimensiones A, B y C deben tener valores próximos.
Comúnmente los valores usados para A,B y C son aproximadamente de 2 a 4 cm.
Para facilitar al máximo la construcción de las bobinas sin la necesidad de muchos cálculos se acostumbra emplear tablas y gráficos en relación a sus dimensiones, espesor del alambre y número de espiras.
Damos a continuación un interesante conjunto de ábacos que pueden ser utilizados para determinar las características de las bobinas.
En la figura 15, mostramos las dimensiones de la bobina usada en nuestros proyectos.
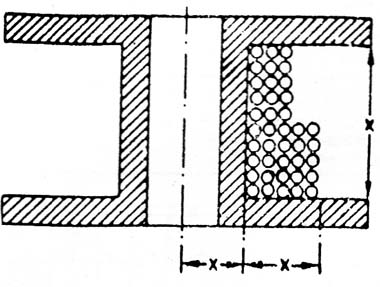
Observemos que fijamos valores X iguales, lo que facilita bastante el proyecto de este componente.
Supongamos, entonces, que la bobina necesaria para la elaboración de un proyecto de divisor de frecuencia, deba tener una inductancia de 1,5 mH.
En el gráfico de la figura 16 debemos buscar el valor deseado en la linea horizontal L (mH). Trazando una vertical a partir del valor indicado, vemos que cruza con las transversales de X en varios puntos (24,5 ; 19,05 : 12,7 , etc.).
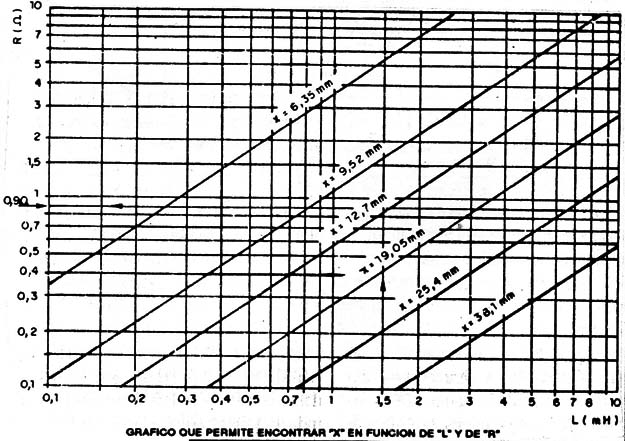
Entretanto, vemos que en los niveles en que ocurren las intersecciones, son diferentes, correspondiendo pués a diferentes resistencias ohmicas.
En la intersección de la linea de 25,4mm, por ejemplo, tirando una horizontal hasta la marcación de R vemos que la resistencia obtenida es de apenas 0,29, en tanto, que en la linea de 19,05mm para X, la resistencia será de 0,49, en la de 12,7mm será de 0,912. La linea de 9,52m no es recomendada para nuestro proyecto, pues ya tenemos una resistencia superior a 1Q.
Para potencias inferiores a 30W, el valor de 0,99 es considerado satisfactorio.
De esta manera tenemos:
R: 0,99
L: 1,5mH
X: 12,7mm
Con estos datos pasamos al giálico de la figura 17.
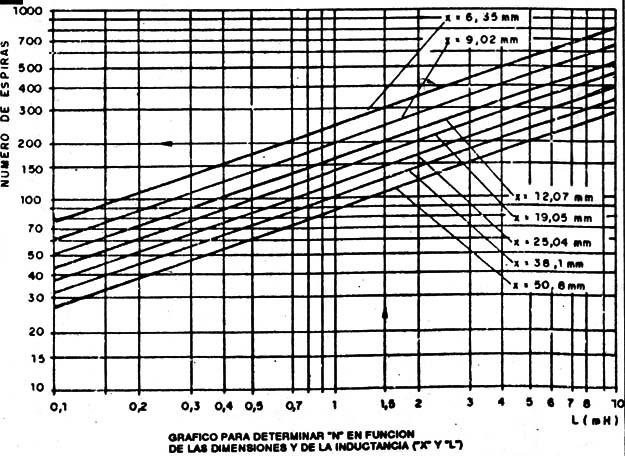
En la horizontal ubicamos el valor de la inductancia deseada que en este caso es de 1,5mH y a partir de este valor trazamos una vertical hasta que intersepte la transversal correspondiente al valor de X, o sea, 12,7mm. A partir de este punto, trazando una horizontal, encontramos el número de espiras a ser bobinadas, en este caso, 200.
La elección impropia de X en el gráfico anterior, puede dar como resultado un número excesivamente alto de espiras (superior a 500 es considerado muy alto), si esto sucediera deberá tomarse un nuevo valor de X, siempre tornando en cuenta que R debe ser inferior a 1 ohm.
Luego de tener el número de espiras, debemos averiguar el diámetro del alambre pasando al gráfico de la figura 18.
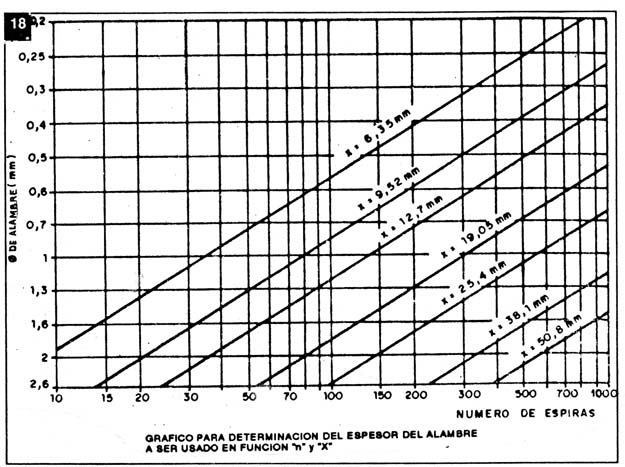
En la horizontal X buscamos el número de espiras determinado (en este caso 200), de allí tiramos la vertical hasta que intercepte la transversal correspondiente a X (12,7mm). Desde este punto trazamos una horizontal, la cual nos dará el diámetro en mm del alambre que será de 0,7mm. Estas dimensiones corresponden aproximadamente a un alambre de 21AWG.
En la tabla 2 podremos seleccionar el alambre en AWG en función de su diámetro en mm. También damos la capacidad de corriente que soportan.
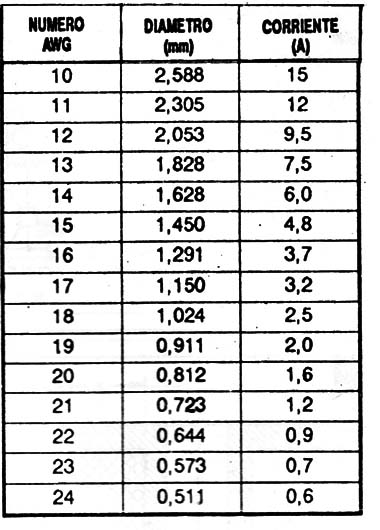
Observemos que la corriente media en un parlante es dada por la potencia del amplificador y la impedancia del sistema. Podemos calcular esto mediante la siguiente fórmula:
I = P / Z
Donde:
I es la corriente en ampere
P es la potencia en watt
Z es la impedancia en ohm
Para un amplificador de 100watt con una carga de 4ohm, la corriente en el parlante llega a los 5 ampere.
Importante:
El trabajo de enrollar las bobinas de acuerdo con lo que deseamos, y después obtener una caja acústica con características exclusivas es un placer que solamente los lectores bien informados y habilidosos pueden tener.





