Este artículo teórico práctico fue escrito en 2006 y actualizado en 2016, pero es absolutamente actual por el tema de que trata. En ello, nos enseña a calcular como se enrollan bobinas (inductores) de valores pequeños, que generalmente se encuentran en transmisores, osciladores, onda corta y receptores VHF, así como instrumentos. Este es el artículo de gran importancia para diseñadores, estudiantes y profesores incluso de cursos de educación técnica y profesional.
Introducción
La mayor dificultad para los que montan circuitos de alta frecuencia tales como osciladores, transmisores, receptores, etc. es cómo conseguir los pequeños inductores o bobinas de que hacen uso estos circuitos, ya que normalmente no se encuentran a la venta en lo comercio especializado. Estos componentes deben ser fabricados por los montadores e son muchos que enfrentan el problema de saber cómo saber cuantas vueltas que necesitamos alambre, de qué manera debe ser enrolado para dada inductancia, e esto es un problema que incluso para muchos profesionales son difíciles de resolver.
Aunque el lector necesita algunos cálculos para llegar al resultado final, en este artículo vamos a intentar hacer las cosas un poco más fáciles para aquellos que quieren enrolar sus propias bobinas.
Una corriente eléctrica que desplazarse a través de un alambre crea un campo magnético alrededor de él, como se muestra en la figura 1.

Este campo magnético tiene propiedades importantes, entre los cuales es oponerse a cualquier cambio en la corriente que atraviesa al conductor que lo crea, ya sea en el momento que se establece el campo, o si es después. Si la corriente tiende a variar, el campo magnético "reacciona" y se opone el ao cambio y induce una corriente en el cable.
Para medir la forma en el campo "reacciona" a las variaciones de la corriente, hay una grandeza, nombrada "autoinducción" o "coeficiente de inductancia", que se mide en Henry (H).
Los submúltiplos del Henry son lo mili Henry (mH) y Micro henrio (?H). La primera es la milésima parte del Henry y el segundo un millonésimo del Henry.
Cuando enrolla los cables para formar una bobina, ocurre el aumento del coeficiente de auto indicación y así podemos obtener componentes electrónicos llamados inductores, bobinas o simplemente "choques", cuyo propósito es presentar una cierta inductancia.
Los principales aspectos de estos componentes se muestran en la figura 2.

Ver que el aspecto está determinado por el número de vueltas de alambre envuelto, la presencia o ausencia de cualquier material que actúe como un núcleo, así como el formato final deseado.
La inductancia, por tanto, dependerá de factores tales, cuando comenzamos a analizar lo siguiente:
a) Formato
La forma de la bobina determina cómo puede distribuir las líneas de fuerza del campo creado por la corriente. Si las líneas producidas por un cable de "escapan" y no tienen acción sobre las bobinas adyacentes de la misma bobina, como ocurre en una construcción más larga cuando (se muestra en la figura 3) tiene una inductancia más baja do que tenemos en una bobina más "apretada".

b) Diámetro
Cuanto mayor sea el diámetro, mayor la inductancia de la bobina, como se muestra en la figura 4.
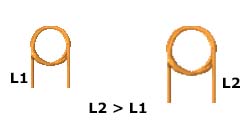
c) Número de vueltas
Cuanto mayor será el número de vueltas de alambre, más líneas de fuerza del campo magnético producido y, por tanto, mayor la "inercia" que presentará el componente frente a variaciones de la intensidad de la corriente.
d) Existencia de un núcleo
Ciertos materiales como, por ejemplo, materiales ferromagnéticos, tienen la propiedad de concentrar las líneas de fuerza de un campo magnético.
Si se coloca dentro de una bobina ellos aumentan la inductancia de esta bobina. Luego podemos aumentar la inductancia de una bobina si introducimos núcleos de materiales ferromagnéticos tales como ferrita, hierro dulce, etc.
La ferrita es una especie de polvo que se compone de diminutas partículas de hierro, que se utiliza en los núcleos de las bobinas que deben operar a altas frecuencias, mientras que el hierro dulce, generalmente aparece en forma de laminado (como en núcleos de transformadores) y es utilizado en las bobinas que funcionan en circuitos de baja frecuencia.
EL CÁLCULO
El principal problema que implica el cálculo de la inductancia de una bobina del tipo indicado en la figura 5, es decir, un solenoide cilíndrico, es que no existe ninguna fórmula absolutamente precisa para eso.
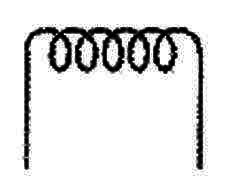
Lo que pasa es que, por más corto que el solenoide o bobina sea, siempre hay líneas de fuerza del campo magnético que "escapan" y por tanto no cortan las vueltas la bobina del mismo, como se muestra en la figura 6.
Cuánto más largo es el solenoide, más líneas de fuerza "escapan" de su parte media, tornando cada vez más difícil aplicar una fórmula con precisión.
Teniendo en cuenta este hecho, lo que hay son fórmulas empíricas o aproximadas que sirven para calcular con razonable aproximación la inductancia de una bobina o solenoide, cuando sus dimensiones cumplen con ciertas condiciones.
Para las fórmulas dadas ser válidas, los solenoides deben ser pequeños, y su longitud no debe ser mayor que dos veces su diámetro o de 1:2. Con el mantenimiento de dimensiones dentro de estos límites, los cálculos son exactos permaneciendo dentro de las tolerancias requeridas por proyectos más prácticos.
Nuestro artículo tiene como objetivo calcular inductores pequeños en la gama de algunos micro Henri unos mili Henry, con la aproximación en los resultados válida para todos los proyectos que suelen encontraron en publicaciones técnicas.
Fórmulas más precisas, que implican cálculo integral puede obtenerse en libros más avanzados de ingeniería.
SIN NÚCLEO
Para solenoides o bobinas cuyas longitudes no son mayores que el diámetro más de 1.5 veces, vale la siguiente fórmula:
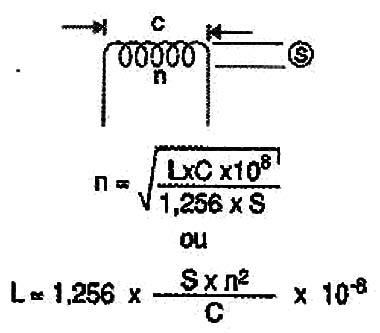
Donde: n es el número de vueltas o arrollamientos
L es la inductancia deseada en Henry
C es la longitud de la bobina en cm (*)
S es el área cubierta por un chapitel (*)
El área cubierta por una bobina se puede calcular fácilmente en función del diámetro de la bobina mediante la fórmula:
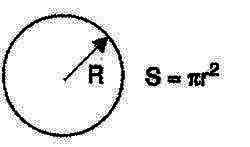
Donde: S es el área cubierta por la bobina en plazas cm
d es el diámetro de la bobina
PI (?) es la constante 3.14
El valor 1.256 es una constante que se obtiene experimentalmente con el fin de adaptar los resultados prácticos obtenidos.
(*)Esta fórmula es válida para solenoides con longitudes en la gama de 0.1 a 2 cm y con diámetros de 0.2 a 1 cm.
Ejemplo práctico:
Calcular cuántas vueltas necesitaremos en un tubo de 1cm d diámetro e 1 cm de longitud para para tener una inductancia de100 µH.
Vea que necesitamos trabajar con ciertas unidades. Por lo tanto, el primer paso para hacer el cálculo es convertir la µH en H.
Para hacer esto simplemente multiplicar por 10 a la potencia de 6.
Tenemos entonces:
L = 100 µH ou 100 x 106
d = 1 cm
C = 1 cm
La fórmula (I), sin embargo, utiliza el área cubierta por una bobina, en lugar de su diámetro. Para calcular el área y nosotros podemos usar este valor en la primera fórmula, tenemos que aplicar la fórmula de segunda.
Tenemos entonces:

Luego debemos tener 100 vueltas en el tubo. La elección del cable depende de dos factores: o elegimos el cable dependiendo de la corriente en el circuito, o para que se mantengan las espiras lado a lado a lo largo. Para los alambres más gruesos, en un caso donde necesitamos mayor capacidad de corriente, podemos tener una bobina "encaballada" como se muestra en (b) en la figura 7.

El caso de bobina superpuesta o encaballadas es más fácil de solucionar ya que acaba de tomar los cables de menor espesor que soporta la corriente deseada.
En el segundo caso, vamos a necesitar todavía de algunos cálculos.
Consultando la tabla de alambres esmaltados, observamos que tenemos una columna con la información de "vueltas por cm". (ver tabla de alambres esmaltados en sitio)
Si vamos a envolver 100 vueltas en 1 cm, es obvio que necesitamos un grosor de alambre en esta condición y las más cercana (111 vueltas por cm) corresponde a lo alambre 40.
Como el cable de 40 es demasiado fino, podemos hacer unas dos capas de la bobina, y así, llegamos a lo alambre 33 que es más fácil trabajar.
Con Núcleo
Con la introducción de materiales ferromagnéticos en un carrete, tenemos una concentración de líneas de fuerza del campo magnético y con que podemos tener una mayor precisión en la obtención de una cierta inductancia, como también podemos hacerlo con menos vueltas.
En el caso de bobinas cilíndricas, núcleo de material ferromagnético tendrá el mismo formato, como se muestra en la figura 8.
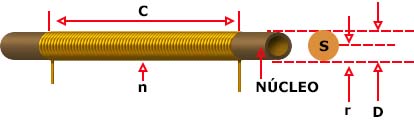
Entra entonces en la fórmula el factor que indica la "concentración" de líneas de fuerza del campo magnético por el material utilizado en la base.
Para el aire, este factor es cercano a 1, mientras que para planchas de materiales este factor puede ser entre 100 y 2000.
Entonces tenemos la fórmula:
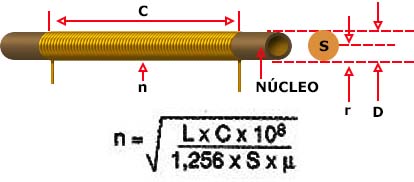
Donde:
n es el número de vueltas de la bobina
L es la inductancia en Henry
C es la longitud de la bobina en cm
S es el área cubierta por la bobina en centímetros cuadrados
u es la permeabilidad del material utilizado en la base
EJEMPLO:
¿Cuál es el número de vueltas que debe ser envuelta en un núcleo de ferrita de 1 cm de diámetro por 2 cm de largo con 2000 de permeabilidad para una bobina de inductancia de 1mH?
Tenemos entonces:
L = 1 mH ou 10 E6
C = 2 cm
µ = 2 000
Utilizar la primera fórmula (II) para calcular (S):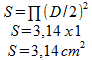
El valor de S, en caso, plazas de 3,14 cm, aplicamos la fórmula (III):
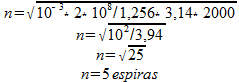
Con la base, necesitamos un número mucho menor de vueltas para obtener la inductancia deseada.
CONCLUSIÓN
El uso de núcleos aumenta la inductancia, pero ofrece otra posibilidad importante para el diseñador. Con un núcleo que se mueve dentro de la bobina, se puede variar su inductancia y así ajustar para el óptimo punto de funcionamiento como, por ejemplo, si usted necesita un circuito resonante.
Por lo tanto, la aplicación, es interesante construir el inductor de una manera que admite un núcleo móvil. Algunos tipos de formas con núcleos móviles están comercialmente disponibles y pueden ser encontradas en televisores y radios antiguas en uso, ya que estas tienen etapas que utilizan estos componentes.





