Las operaciones
Como hemos visto en la lección anterior, la finalidad de un ordenador analógico es realizar operaciones matemáticas usando tensiones (magnitudes analógicas). Las computadoras analógicas modernas se basan en amplificadores operativos, pero existen otros circuitos e incluso componentes que se pueden utilizar en cálculos que involucran magnitudes analógicas.
Por ejemplo, los potenciómetros ¿Sabía qué potenciómetros pueden hacer cuentas?
Lo que vamos a hacer ahora es entrar en una parte práctica de nuestro curso en el que, para aprender cómo funciona un ordenador analógico vamos a enseñar a montar uno usando potenciómetros.
Los lectores podrán perfeccionar este proyecto e incluso incluir características más modernas como el uso de amplificadores operativos, en especial tipos que hoy están disponibles y que permiten obtener una precisión mayor de cálculo.
El potenciómetro haciendo cuentas
Si la idea básica es representar cantidades por una tensión, todo lo que necesitamos, en primer lugar, es tener una tensión estándar. Esta puede venir de una batería de tensión V1, como muestra la figura 1.
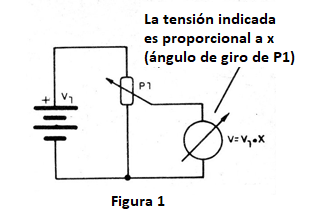
Si conectamos un potenciómetro como muestra esta figura, la tensión que tendremos entre su cursor y el terminal negativo dependerá de su posición o giro.
Así, podemos girar el eje del potenciómetro para representar cualquier cantidad entre 0 y V1. Suponiendo que V1 sea 1 volt, podemos decir que este circuito representa cualquier cantidad de X entre 0 y 1. Conectando un indicador de tensión en el cursor de este potenciómetro, marcará un valor proporcional al ángulo que girar el eje del potenciómetro.
Recordemos que el potenciómetro consiste en una resistencia que puede cambiar de valor por el movimiento de un cursor, como muestra la figura 2.
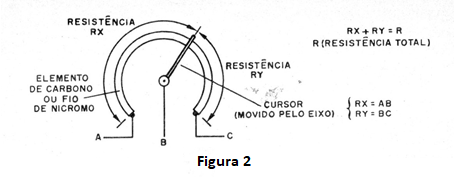
Dependiendo de la posición del cursor, la resistencia entre A y B y entre B y C varía. Así, el potenciómetro conectado de la forma mostrada en la figura 1 forma un divisor de tensión, es decir, un circuito que divide la tensión de la batería de modo que quede entre 0 y 100% del máximo.
Pero, un potenciómetro solo no es suficiente para la realización de operaciones. Supongamos que se conectan dos potenciómetros de la manera mostrada en la figura 3.
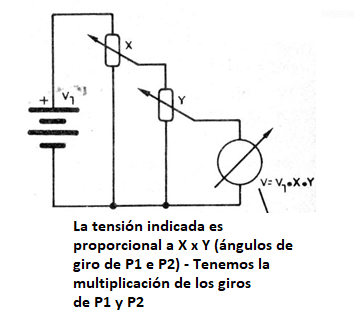
El cursor de X nos permite tomar una fracción de la tensión de entrada. Vamos a suponer que este potenciómetro está dotado de una escala calibrada de 0 a 1. Esto significa que, moviendo el eje de este potenciómetro, podemos "recoger" cualquier cantidad entre 0 y 1.
Pues bien, el segundo potenciómetro, marcado como Y, permite hacer lo mismo con respecto a X, es decir, podemos tomar cualquier fracción entre 0 y 1, pero de lo que sea retirado de X.
Si el cursor de X está en 0,5 y llevamos el cursor de Y a 0,6, el resultado que tendremos será 0,5 de 0,6, es decir, 0,5 x 0,6 = 0,30. Tendremos entonces al final una tensión que corresponde a 0,30 de la tensión de entrada y habremos realizado una multiplicación! Dos potenciómetros conectados de la manera indicada multiplican cantidades;
Es claro que a partir de la multiplicación podemos hacer otras operaciones, pues: dividir y multiplicar por lo inverso; elevar al cuadrado es multiplicar un número por él mismo, y así sucesivamente.
Pero todavía existe un problema a resolver:
El detector de nulo
No es muy interesante tener un indicador de tensión para marcar el resultado de la operación. Una manera más interesante es también utilizar un potenciómetro con una escala que tenga el resultado en algún punto.
Así, una vez que hayamos propuesto el problema, basta girar el potenciómetro de respuesta hasta que el resultado sea alcanzado. Y claro que para eso hay que haber algún tipo de indicador que avise cuando este resultado sea encontrado. Una manera simple de hacer esto se muestra en la figura 4.
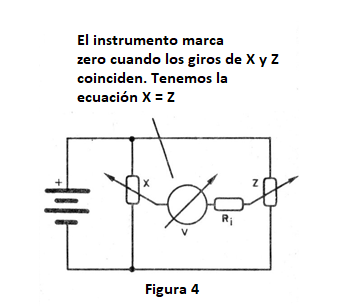
Si el potenciómetro X tiene su cursor ajustado a una cierta posición que resulta en una tensión en V, girando el potenciómetro 2 vamos, en determinado momento, a encontrar una posición en la que tendremos la misma tensión.
De este modo, la tensión en el instrumento se anula y esto ocurre para un solo valor. En el circuito de multiplicación, como muestra la figura 5, tendremos entonces 3 potenciómetros.
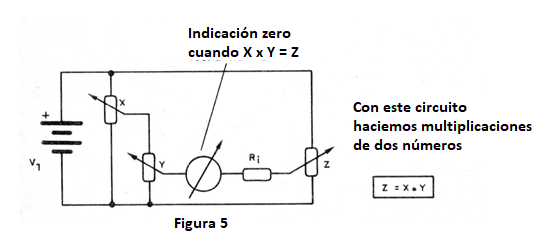
Los dos primeros corresponden a los datos del problema, es decir, los valores que deben ser multiplicados, divididos, etc. El tercero, marcado con Z, sirve para poner a cero el instrumento, encontrando la respuesta.
Así, la operación se vuelve simple. Si queremos multiplicar 0,5 por 0,6, ajusta X en 0,5 del giro, Y en 0,6 del giro y luego vamos girando el eje de 2 hasta que el instrumento indicador de nulo marque cero. En este momento leemos en la escala de Z el valor 0,30 con certeza!
En la figura 6 tenemos una configuración con 4 potenciómetros, que permite trabajar con tres valores.
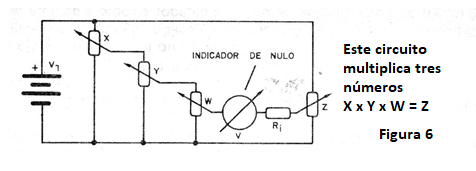
Ver que si queremos operar con dos números en este ordenador, bastará llevar el potenciómetro X a 1, pues 1 multiplicado por alguna cantidad es igual a esta cantidad y simplemente considerar Y veces W !.
¿Qué tipos de operaciones se pueden hacer?
Además de las cuatro operaciones, con 3 potenciómetros podemos hacer los siguientes tipos de cálculos:
- potenciación;
- radiación;
- cálculo de senos y cosenos de ángulos;
- solución de ecuaciones simples.
Podemos comparar este aparato a las reglas de cálculos, con la diferencia de que en lugar de lentes de cursor tenemos potenciómetros con. sus cursores, pero que llegan a los mismos resultados.
Consideraciones sobre la precisión
Un problema importante que ocurre en el diseño y operación de este tipo de equipo es la introducción de errores. Cuando trabajamos con. los circuitos digitales, la introducción de errores casi no ocurre, porque las variaciones de tensión en el circuito no afectan el resultado. Una tensión que varía entre 3 y 5,5 V se interpreta como 1 por un circuito, del mismo modo que una tensión entre 0 y 0,7 V se interpreta de forma segura como "0".
En el caso de un ordenador analógico, las variaciones, por menores que sean, afectan los resultados. Si queremos representar la cantidad 3,1 y llevar el cursor del potenciómetro hacia un poco más allá o un poco antes de esta posición en la escala, tendremos 3,2 o 3,0 o cualquier valor intermedio, pues este tipo de máquina no reconoce cantidades discretas , es decir, no trabaja sólo con valores enteros.
Esto significa que la precisión de los componentes, principalmente la tolerancia del potenciómetro y su linealidad, son factores que influyen en la realización práctica de un proyecto preciso.
De la misma manera, cuando conectamos un potenciómetro a otro, como muestra la figura 7, un "carga" el otro, en el sentido de que pasamos a tener en la rama inferior RX2 la conexión de una resistencia RY que cambia su valor.
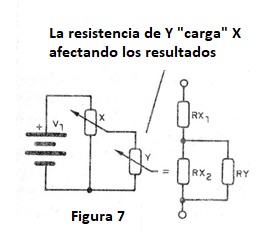
Para que esto no ocurra, RY debe ser mucho mayor que RX.
Cuanto mayor sea RY en relación a RX, mejor es la precisión del ordenador, pero en compensación se requieren detectores de nulo más precisos.
En suma, la precisión de este ordenador es como la de una regla: depende no sólo de su calidad, como también del manejo y de la propia lectura.
Con componentes comunes, comprados en tiendas, se puede tener una precisión de 2 a 5%, lo que no puede ser comparado a la de una calculadora (que llega a ser absoluta!), Pero sirve para ilustrar el funcionamiento del circuito.
Lo mismo ocurre con los ordenadores analógicos que utilizan amplificadores operativos. Los componentes del circuito no presentan precisión absoluta. Los resistores, por más precisos que sean, llegando en algunos casos al 0,1% suman sus imprecisiones a medida que la señal pasa de paso a paso.
Sin embargo, es interesante observar que en muchos sistemas naturales que trabajan con señales analógicas la imprecisión existe y se considera natural. No podemos diferenciar con precisión dos tonos de frecuencias cercanas, ya que nuestro sistema auditivo es analógico.
La naturaleza se adapta a la operación con señales analógicas sin problemas. Es por ese motivo que los investigadores que trabajan con la bión y la inteligencia artificial están cada vez más mirando con cuidado para la computación analógica en sus trabajos.
Otros detectores de nulo
En los ejemplos que dimos, usamos un instrumento para indicar el punto en que la respuesta era alcanzada, porque trabajamos con la tensión de una pila. Sin embargo, existen otras posibilidades de uso de detectores e incluso de fuentes de tensión.
Por ejemplo, pera hacer el circuito más sensible, de modo que no afecte la precisión del resultado podemos conectar el instrumento a un amplificador transistorizado. Otra posibilidad, que lleva a mejores resultados, es usar un amplificador operacional, como muestra la figura 8.
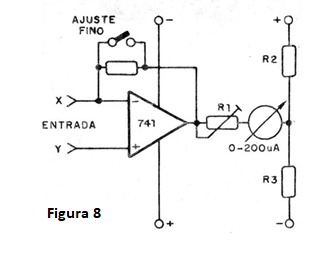
En este caso, como la amplificación del operativo y muy grande, en lugar del instrumento podemos usar LEDs. El apagado de los dos LED muestra el punto de equilibrio.
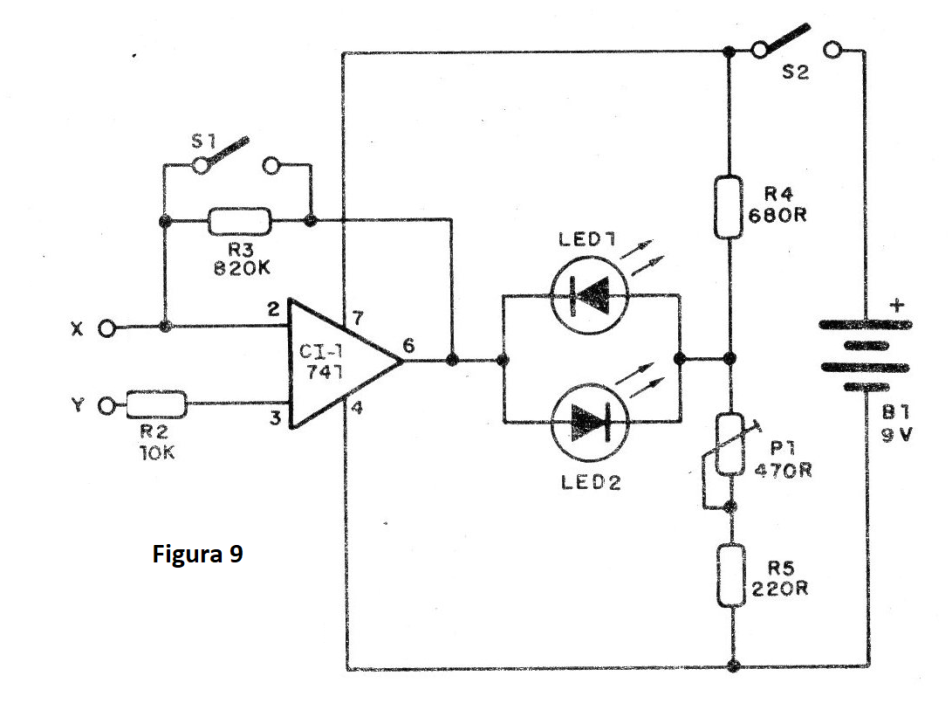
En la figura 9 tenemos un ejemplo de un circuito de indicador de nulo que hace uso de LEDs en oposición.
En este circuito cuando la tensión en el pin 6 es mayor que la mitad de la tensión de referencia, ajustada en P1 y dada por las resistencias R4 y R5, se enciende el LED2. Cuando es menor, se enciende el LED1.
Como la ganancia del funcionamiento depende de la retroalimentación, podemos incluso colocar una llave que permite aumentar la ganancia a medida que nos acercamos a la solución del problema (punto de equilibrio) y con ello elevar la precisión.
También podemos trabajar con señales de audio en lugar de tensiones continuas. Sustituimos la pila (o batería) por un oscilador de audio y el detector de nulo pasa a ser un auricular o un amplificador conectado a un altavoz. (figura 10)
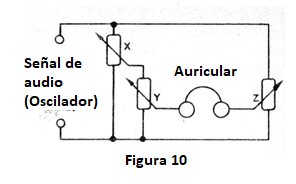
El auricular es ideal para este tipo de detección, por su alta impedancia.
No necesitamos decir que el montaje de un ordenador analógico consiste en una excelente sugerencia de trabajo escolar.
Antes de la segunda guerra mundial, los ordenadores analógicos de gran tamaño ayudaron en la elaboración de tablas de tiros y de muchos trabajos que hoy se pueden hacer incluso por pequeños ordenadores. En aquella época las escuelas también tenían sus microcomputadoras analógicas, como lo que describimos, y que eran usados no sólo en la enseñanza de las matemáticas en sí, sino también en la introducción de la informática de la manera en que tendía en aquellos tiempos.
No queremos decir que el ordenador analógico deba ser olvidado, pues su importancia didáctica es infinita. Por el contrario, publicando artículos sobre este equipo, esperamos que sea colocado en el lugar que le corresponde: enseñar a los jóvenes en las escuelas.
Tipos de Potenciómetros
En los proyectos de computadoras analógicas y cualquier otro que haga uso de potenciómetros usamos normalmente los tipos de 270 grados que siempre.
Sin embargo, no son únicos que se pueden obtener actualmente. Además de los tipos deslizantes tenemos otros como lo que describimos a continuación.
¿Usted ya necesitó para un uso de un potenciómetro "sin fin" o "endless" que pueda girar continuamente la rotación completa de 360 grados? Sí, este componente existe. Es el potenciómetro Endless y Piher los fabrica. En este artículo tratamos un poco de este componente que puede ser de gran utilidad en un proyecto de automatización.
(*) Este artículo se basa en el datasheet del ST-15, potenciómetro Endless de Piher que se puede adquirir en Mouser Electronics en el enlace: https://www.mouser.com/new/piher/piher-st-15-rotation- potenciómetros /.El datasheet, a su vez, se puede acceder en el enlace: https://www.mouser.com/datasheet/2/325/ST-15-1368214.pdf
Los potenciómetros comunes tienen un giro definido, normalmente llegando a los 270 grados, obteniéndose así una banda de control que no es total si se tiene en cuenta el giro posible del eje, como muestra la figura 11.
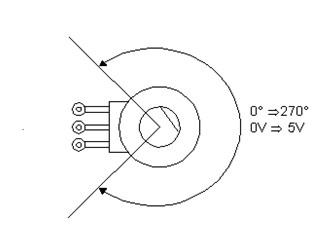
En muchas aplicaciones que involucran el uso del potenciómetro para el sensor, este ángulo no es problema, pero puede ser que ocurra la necesidad de obtener un sensor en el giro completo y, más que eso, que el potenciómetro pueda ser libre dando vueltas "sin detener".
Para este propósito se debe utilizar un pote con características especiales que es el llamado "endless" o sin fin. Phier, cuyos componentes se pueden adquirir en Mouser Electronics, ofrece una línea de potenciómetros de 360 ??grados de 15 mm. La serie ST-15 se puede encontrar con valores de 1 k a 100 k en la serie de 1 - 2 - 2,2 - 2,5 - 47, y 5).
En la figura 12 tenemos los aspectos de estos componentes.
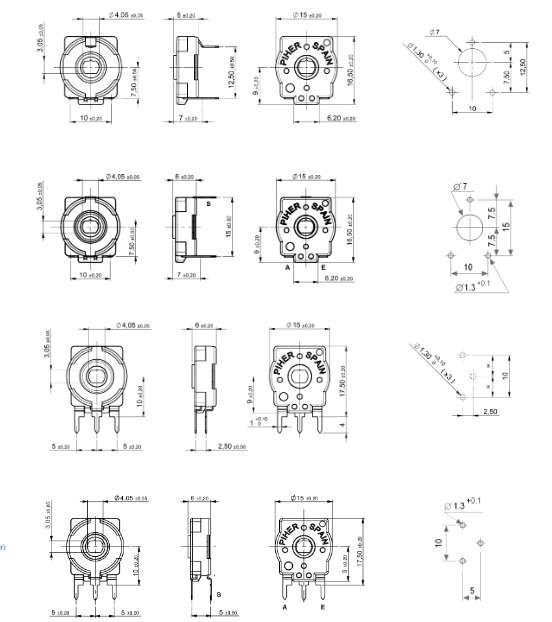
Y para facilitar el uso en una aplicación el fabricante también ofrece prolongaciones, ejes y otros recursos mecánicos de acoplamiento a su sistema, mostrados en la figura 13.

Ciertamente estos potenciómetros pueden servir de base para un proyecto de computadora analógico interesantes.
En la tercera lección de este curso muy rápido vamos a enseñar al lector a montar un pequeño ordenador analógico didáctico experimental que funciona como una regla de cálculo electrónico.
La precisión dependerá de la tolerancia y calidad de los potenciómetros usados y con imaginación el circuito puede ser ampliado para más cálculos con la utilización de más potenciómetros y de conmutadores.
Sumário
Computación Analógica - Lección 1
Computación Analógica - Lección 2