Hacer Cálculos
En las lecciones anteriores aprendemos cómo funcionan las computadoras analógicas y específicamente como potenciómetros pueden ser usados para construir un ordenador simple capaz de realizar operaciones básicas usadas en matemáticas.
A continuación, aprendemos cómo montar un circuito práctico de una pequeña computadora experimental capaz de hacer diversas operaciones. En el análisis básico de su funcionamiento quedó claro cómo podemos hacer multiplicaciones. En estas lecciones le mostraremos cómo hacer otras operaciones.
Revisemos, sin embargo, la operación de la multiplicación mostrando cómo se puede hacer.
a) Multiplicación
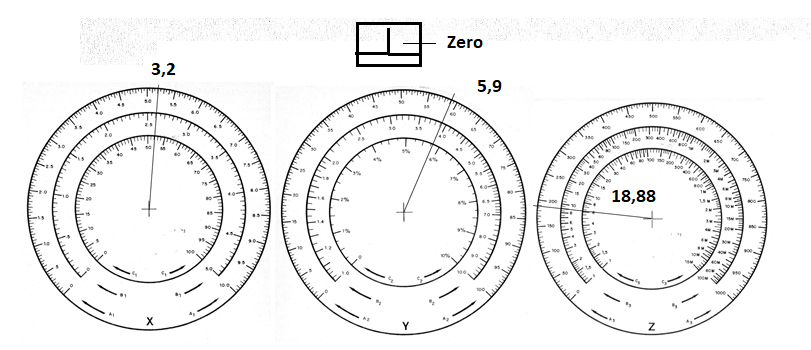
Supongamos que deseamos hacer una multiplicación simple como 3,2 x 5,9;
En este caso tenemos:
X = 3,2
Y = 5,9
Z = resultado de la operación
El primer procedimiento es colocar en la escala el valor de la forma que sea más próxima que la escala usada suporte. Observe que la escala lineal va hasta 10. Así, tenemos en la figura el ajuste de X para este valor.
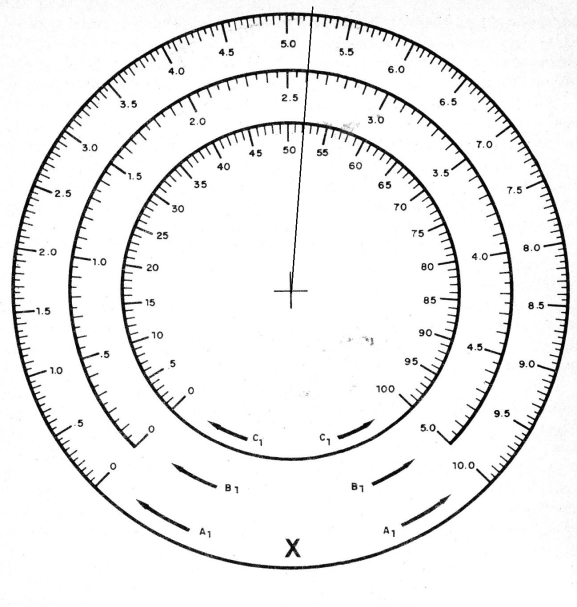
El segundo paso es ajustar el valor 5,9 en la escala Y. Procedemos de la misma forma que en la escala X, como muestra la figura 2.
Ver que ajustaríamos ese mismo punto si tuviéramos que trabajar con números más grandes, compensando los ceros. Por ejemplo, esto sería válido para la multiplicación: 32 x 59 = Y
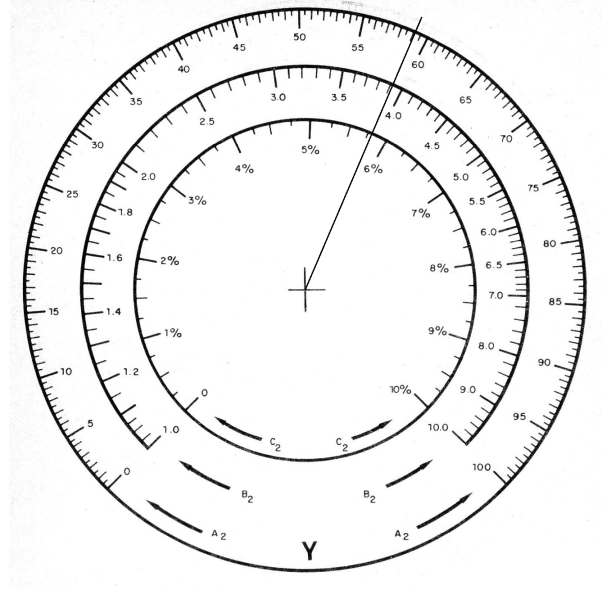
Ahora, en la etapa final, vamos a accionar el circuito y girar Z hasta que el instrumento sea cero. Esto ocurrirá justamente en el punto 18,88, como muestra la figura 3.
Ver que en este caso tenemos que hacer una compensación de las escalas, deduciendo de cabeza que el valor encontrado esta aproximadamente en este punto y que debemos desconsiderar un cero en el resultado de la operación.
Como en las reglas de cálculo, el orden de magnitud tanto de los operandos como de los valores encontrados depende mucho más del operador que del propio dispositivo utilizado en el cálculo.
Otro punto importante a considerar es la precisión de los resultados. El valor 18,88 no se puede leer con precisión en la escala externa utilizada de la misma forma que los valores de los operandos.
Así, este tipo de calculadora no es para valores que exijan precisión, funcionando más con pequeños valores enteros. Se tiene en cuenta la tolerancia de los potenciómetros.
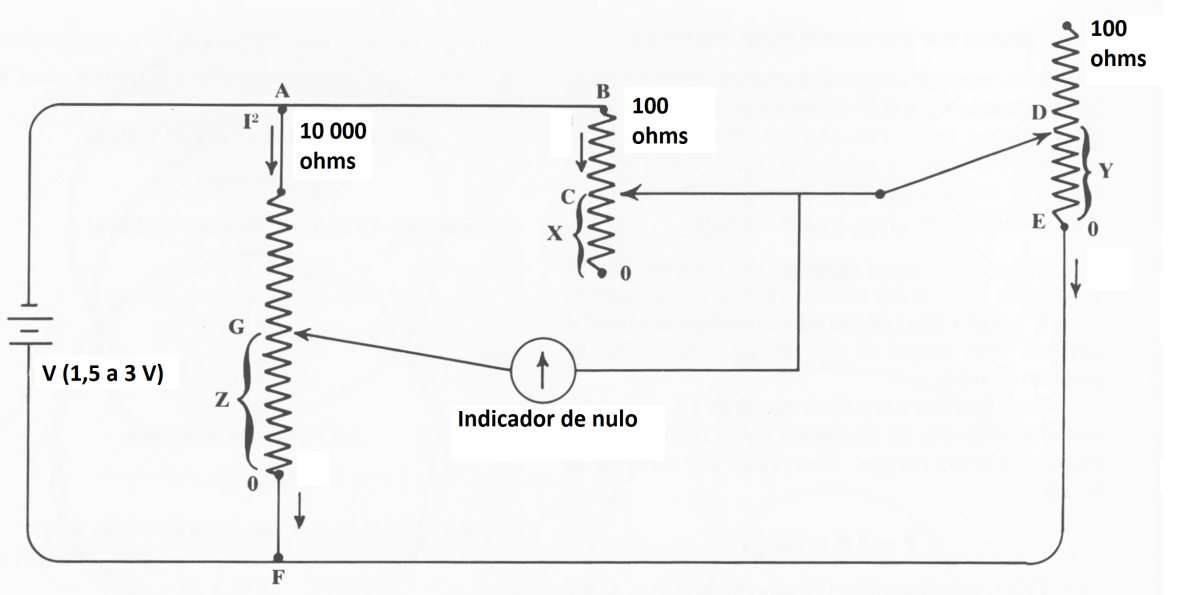
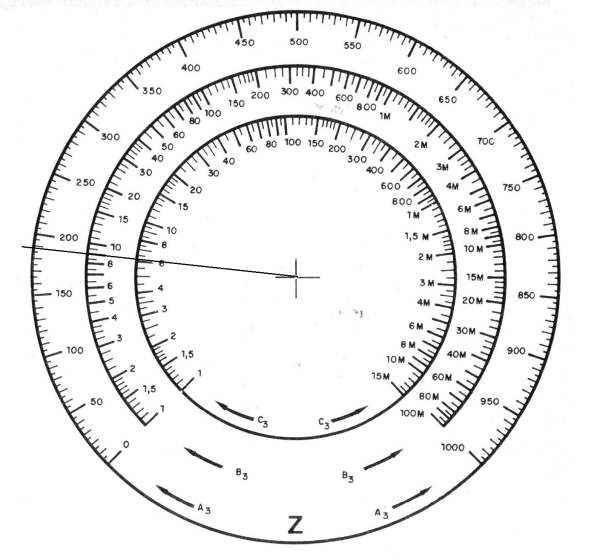
El resultado final se muestra en la disposición final de los potenciómetros según se detalla en la figura 4.
Para las otras operaciones el procedimiento es básicamente el mismo, por lo que no necesitamos ilustrar con figuras. Sólo diremos qué escalas se utilizan.
b) Dividir
Considerando que la división es un procedimiento inverso al de la multiplicación el lector puede fácilmente deducir cómo realizarla en su computadora analógica.
Suponiendo que vamos a dividir 9 por 2.
En este caso, invertimos el procedimiento, colocando el 90 en la escala Z y el 20 en la escala Y.
Z = 90
Y = 20
X =?
El resultado se obtendrá en la escala X cuando giremos el potenciómetro y obtengamos el cero del instrumento.
Vea que también en este caso debemos considerar los puntos en que los valores serán ajustados.
Para 90 usamos 9, para 20 usamos 2 y el resultado no será obtenido en 45 pero sí y 4,5.
c) Potencias
Elevar un número al cuadrado, consiste en multiplicarlo por él mismo. Por ejemplo:
32 = 3 x 3 = 9
Así, para elevar al cuadrado, basta ajustar el mismo número en la escala x y en la escala Y encontrando la respuesta en la escala Z.
Elevar 4 al cuadrado, por ejemplo:
X = 4
Y = 4
Encontraremos Z = 16 cuando el instrumento sea cero.
Para otros exponentes ya tenemos un procedimiento que exige un poco más de habilidad. Por ejemplo, vamos a elevar 43.
En este caso, tenemos:
4 x 4 x 4
Entonces hacemos la primera multiplicación usando los potenciómetros x e y. Obtenemos el valor 16 en Z. Ajustamos nuevamente Y para el valor encontrado en Z y de nuevo ajustamos Z para un nuevo cero.
El valor encontrado será 4 x 4 x 4 = 64 o 43.
Para exponentes mayores también podemos usar las escalas intermedias B trabajando como si fueran multiplicaciones. Ver más adelante porque eso es posible.
d) Raíz cuadrada
La raíz cuadrada de un número a es el número b que multiplicado por él mismo resulta en a.
Por ejemplo, la raíz cuadrada de 9 es 3 porque 3 x 3 = 9. La raíz cuadrada de 16 es 4 porque 4 x 4 = 16.
Para calcular la raíz de un número en nuestro conmutador analógico utilizaremos las escalas de la banda intermedia B. Así, si queremos calcular la raíz de 9, ajustamos 9 en la escala B de X. Luego ajustamos nuevamente 9 en la escala B de Y y encontramos el resultado aproximado en la escala B de Z.
¿Por qué el resultado de las raíces se obtiene en estas escalas?
Para que el lector entienda debe conocer un poco sobre logaritmos.
Si tenemos los números a, b y c y realizamos la operación tal que ax = b, podemos decir que x es el logaritmo de b en la base a o:
X = loga b
Una escala logarítmica en que las divisiones se separan de forma exponencial, tienen propiedades interesantes cuando se usan en un ordenador como el nuestro.
Por ejemplo, vemos que la suma de los logaritmos de dos números es igual al logaritmo de su producto. En otras palabras, podemos multiplicar usando la suma.
De la misma forma, para obtener una potencia, basta multiplicar el logaritmo de la base por el logaritmo del exponente. En otras palabras, podemos calcular exponentes usando la multiplicación.
Como la raíz cuadrada es el inverso de la potenciación, usando un escalas logarítmicas podemos hacer su cálculo utilizando la división.
Así, la raíz cuadrada de un número se puede encontrar dividiendo el logaritmo de ese número por el logaritmo de 2. Las escalas B de nuestro ordenador sirven justamente para hacer esos cálculos usando logaritmos.
Pero lo interesante es que, como trabajar con magnitudes analógicas podemos ir mucho más allá de lo que sería posible con una calculadora digital.
Podemos elevar un número a un exponente no entero como 30,4 o aún la raíz "1,3" de 2.
Cálculos Complejos
Es claro que, a medida que el lector es adquiriendo experiencia con su computadora analógica puede ir entendiendo cómo realizar más cálculos. Por ejemplo, puede crear nuevas escalas, colocando por ejemplo funciones trigonométricas y trabajando con ellas.
Basta recordar que el circuito multiplica y que por lo tanto podemos realizar esta operación con los valores de las escalas. Si estas escalas se elaboran sobre la base de otras funciones, sus características se añaden al circuito.
Por ejemplo, si tenemos una escala que sigue la función "seno de un ángulo" en X y "coseno" en Y podremos multiplicar los senos por cosenos, bastando elaborar una escala apropiada en Z.
Otra posibilidad consiste en modificar la forma en que se encienden los potenciómetros. En la figura 5, por ejemplo, tenemos una variación que nos lleva a la fórmula de actuación del circuito como:
z = [ 10Y / (1 – X + 10Y) ]
Un sistema de conmutación interno puede llevar a las diversas configuraciones del circuito.
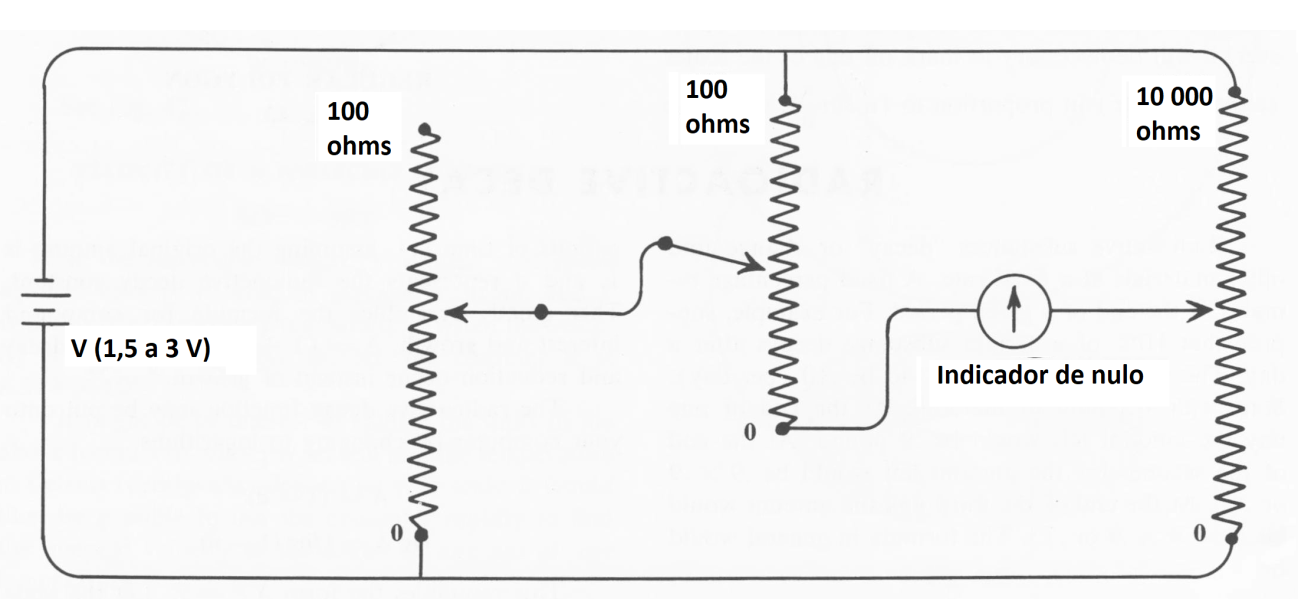
Otra posibilidad interesante se muestra en la figura 6, siempre teniendo en cuenta que la relación de valores entre los potenciómetros de alta y de baja resistencia debe ser mantenida la más alta posible para obtener más precisión.
Al analizar este circuito el lector puede llegar a la ecuación que describe su operación. Así, de la misma forma que en un ordenador analógico con amplificadores operativos, diferentes disposiciones de potenciómetros pueden ser creadas para realizar los cálculos específicos que deseamos.
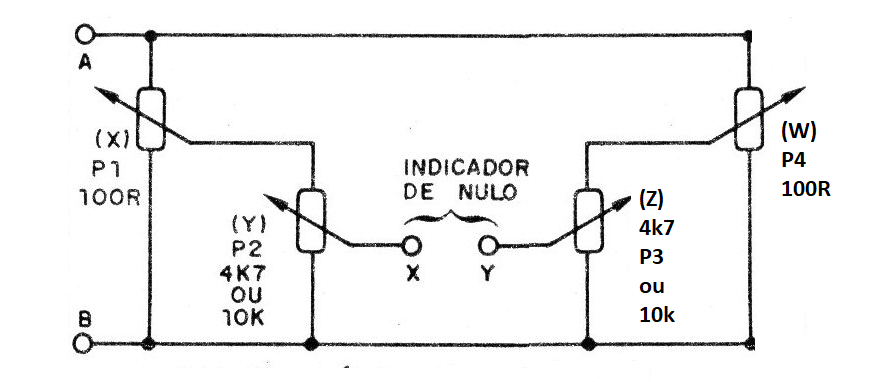
También tenemos la posibilidad de aumentar el número de potenciómetros, como muestra la figura 7.
En este circuito tenemos la posibilidad de resolver ecuaciones del tipo:
X x Y = W x Z
Para operaciones simples, como las normales, basta colocar W en el punto de máxima resistencia (Cursor en + B) de la alimentación y circuito pasa a tener la condición de Z = 1 llevando a:
X x Y = Z x 1
o
X x Y = Z
Que es la versión original.
Sin embargo, la ventaja de este circuito es que podemos resolver proporciones con él, calculando por ejemplo la cuarta proporcional en la fórmula:
X / Y = W / Z
Esta posibilidad de incrementar el proyecto, ciertamente puede ser atractiva para los lectores que deseen saber más sobre ordenadores analógicos.
Podemos incluso trabajar con seis potenciómetros siendo 3 en cada rama obteniendo así la ecuación de funcionamiento:
X x Y x Z = X1 x Y1 x Z1
El tercer potenciómetro de 100k o 1 M se conectar en el cursor de Y.
En la figura 8 tenemos un circuito para X x Y x W = Z
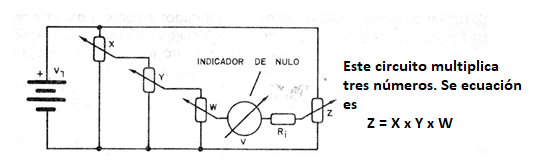
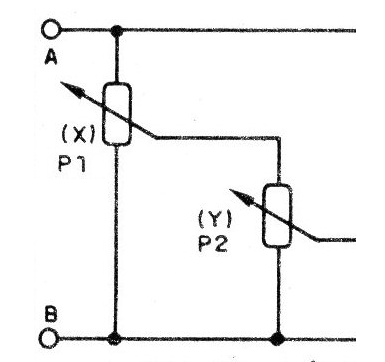
Debemos siempre recordar que en la elección de los valores de los componentes el potenciómetro de carga (que carga el divisor principal) debe ser lo más grande posible por los motivos que ya analizamos en las lecciones anteriores de nuestro curso.
En el circuito de la figura 9 P2 debe ser el mayor posible en relación a P1 para no "cargarlo" formando un divisor de tensión que afecta los resultados del circuito.
Sumário
Computación Analógica - Lección 1
Computación Analógica - Lección 2