La mayoría de los circuitos electrónicos trabajan con señales que corresponden a corrientes alternas de diversas frecuencias. Por una señal entendemos una corriente que varía periódicamente de intensidad cambiando, por ejemplo, de polaridad a intervalos regulares.
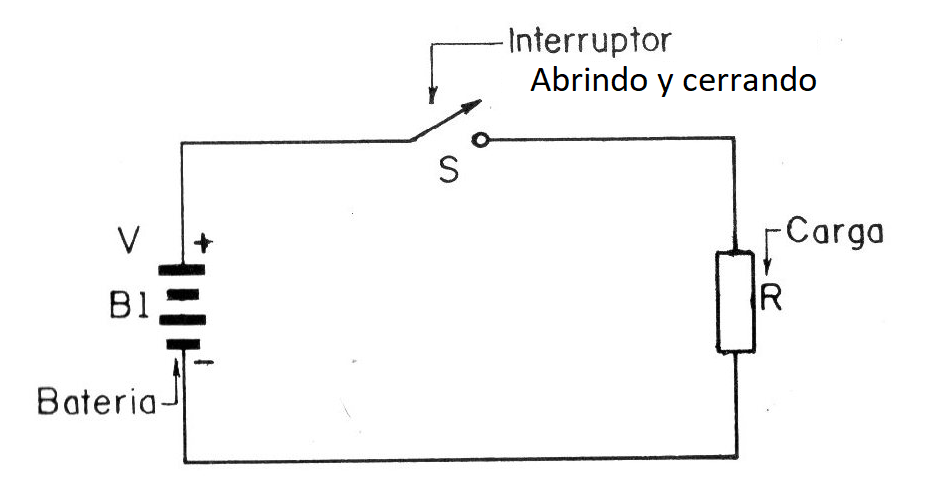
Si abrimos y cerramos un interruptor rápidamente, para tener tensiones producidas a intervalos regulares en un circuito de carga, como se muestra en la figura 1, estaremos generando una señal.
Las características de una señal pueden ser dadas de diversas formas:
a) La frecuencia, que es el número de veces en cada segundo en que se repiten los valores de tensión o corriente. En el caso de la clave tomada como ejemplo, la frecuencia será dada por el número de veces en cada segundo que la cerramos (o abrimos).
b) La forma de onda que es más importante, en nuestro caso, pues dice de qué modo la corriente o la tensión varían en un determinado intervalo de tiempo considerado.
Para entender mejor lo que viene a ser la forma de onda, será interesante definir también lo que viene a ser período y un ciclo de la señal.
En el caso de un interruptor que se abre y cierra, si partimos del instante inicial en que está abierto, y luego lo cerramos, cuando lo abrimos nuevamente habremos completado un c1clo de su operación.
Cerrando nuevamente este interruptor el ciclo se repite y así indefinidamente mientras actuamos sobre él.
En el caso de que se produzca un cambio en el circuito de carga formado por una resistencia R, vemos que en un ciclo tenemos dos situaciones:
Fase inicial en que la tensión en la carga es nula.
Fase final en que la tensión es máxima.
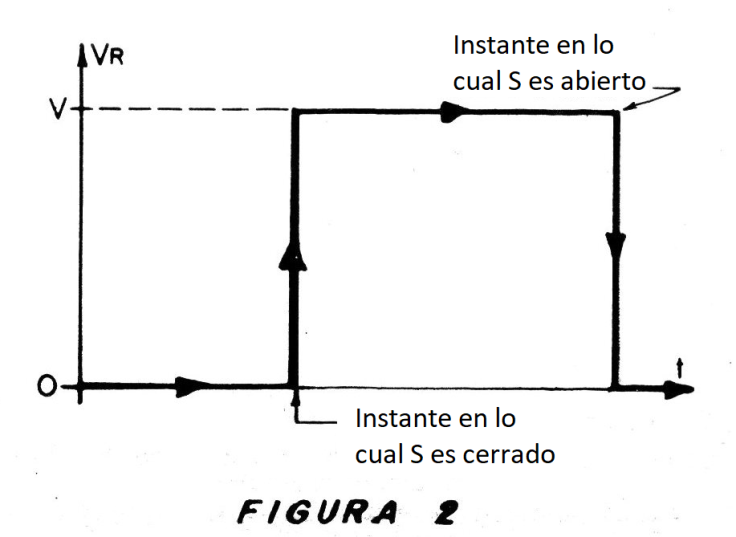
La subida de la tensión en la carga de cero al valor máximo puede ser considerada instantánea. Ver la figura 2.
Observando la figura que el gráfico forma vemos que se asemeja al escalón de una escalera con una transición rápida de lo hasta el máximo.
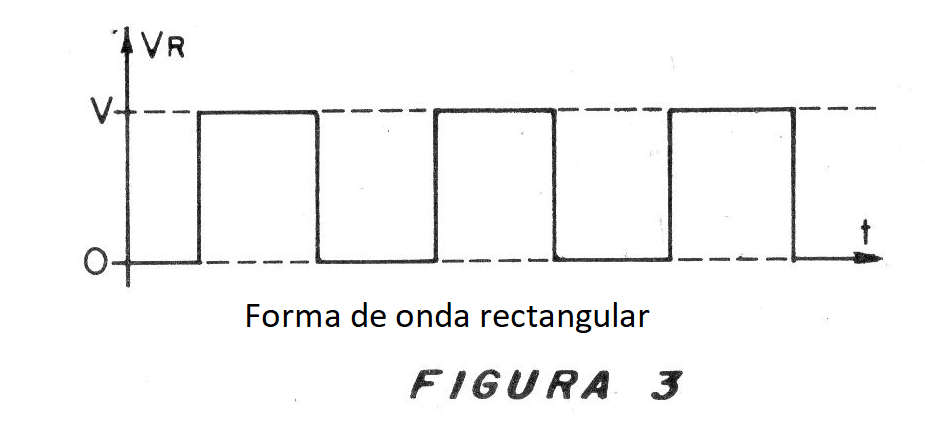
Si representamos varios ciclos a continuación, como muestra la figura 3, tendremos un "retrato" de esta forma de onda peculiar que representa variaciones rápidas de la corriente o tensión en R.
Esta forma de onda se denomina "rectangular", pues los ciclos tienen este formato geométrico en su representación.
Es interesante observar que la corriente que corresponde a una señal de este tipo físicamente no tiene nada de rectangular, pues ni siquiera tiene forma definida. Se trata de un flujo de electrones que no tiene masa perceptible y no puede ser visto, por lo que no puede definirse la forma.
El nombre dado a este tipo de corriente que tiene variaciones bruscas viene de su representación gráfica que, como vimos, es correspondiente a rectángulos.
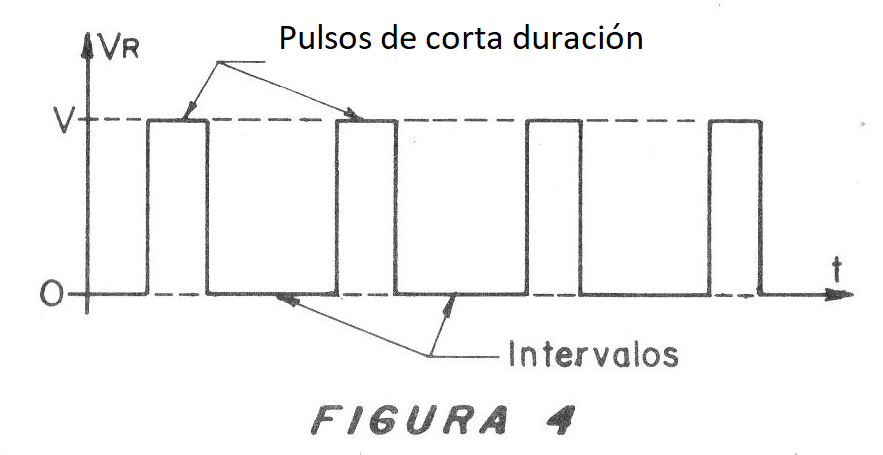
En la figura 4 tenemos un tipo de forma en que los intervalos son mayores que los pulsos en su duración.
Esta es también una forma de onda rectangular.
Vamos a suponer ahora otro tipo de corriente que también corresponde a una señal.
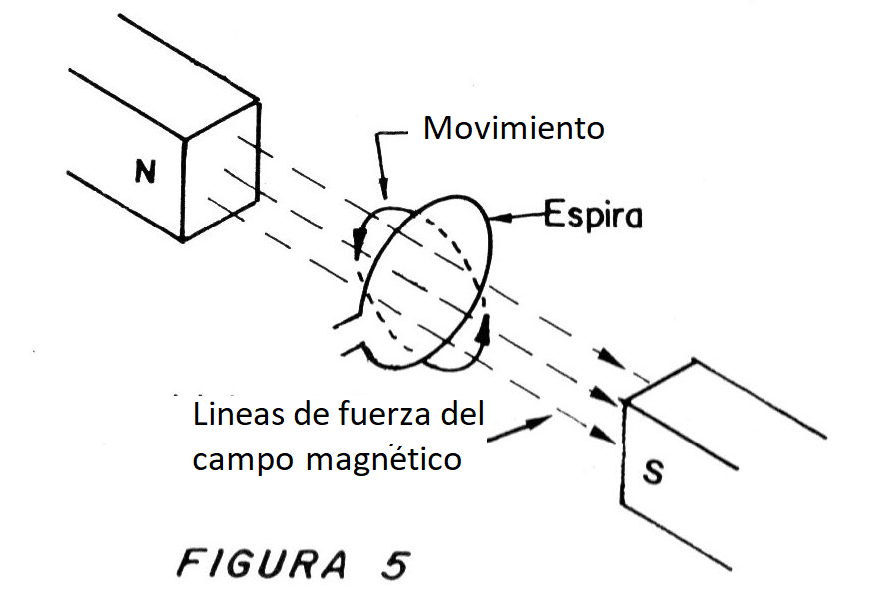
Imaginemos una espira de hilo conductor que corta en un movimiento circular las líneas de fuerza de un campo magnético, como muestra la figura 5.
Lo que tenemos en esta estructura es un generador de corriente alterna que genera un tipo de señal muy especial. Cuando la espira gira y entra en el campo magnético, cortando las líneas de fuerza, es inducida una tensión que crece suavemente de valor hasta alcanzar el máximo a 1/4 de la vuelta completa.
A partir de este punto, la tensión generada en suavemente hasta alcanzar nuevamente el punto mínimo (cero) en 1/2 vuelta.
Continuando con el movimiento, la tensión nuevamente aumenta suavemente de valor, pero como el movimiento ahora corta las líneas de fuerza en el sentido contrario, la tensión es negativa. A 3/4 de vuelta la tensión negativa alcanza su punto máximo, para caer nuevamente a cero en la vuelta completa.
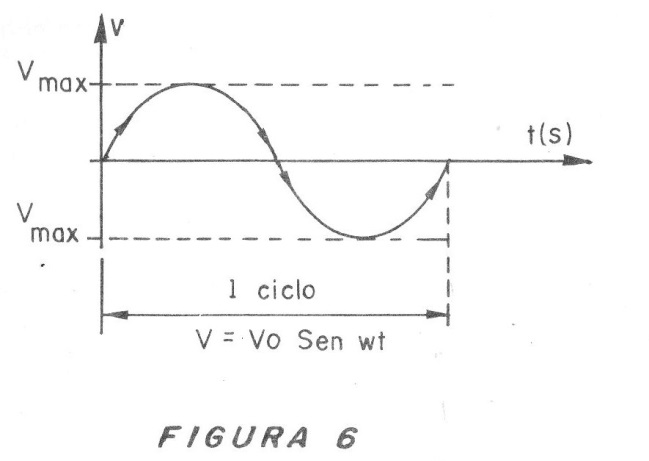
Si representamos la tensión generada por este movimiento de la espira en un gráfico, tendremos una curva suave, como muestra la figura 6.
Esta curva puede ser expresada por una función matemática denominada sinusoidal que asigna un valor a cada ángulo de la vuelta. Decimos entonces que la forma de onda de esta corriente es senoidal.
La corriente alterna que obtenemos en la toma de fuerza de nuestras casas tiene forma de onda senoidal, pues los generadores que las producen operan según el mismo principio de la espira que tomamos como ejemplo.
Es claro que la corriente en sí, nada tiene de senoidal, pues ella no puede ser vista, pero su representación lleva a una figura que es una sinusoide, de ahí decir que la forma de onda corresponde a la sinusoide.
La frecuencia de la corriente alterna de la red es 60 hertz (60 ciclos en cada segundo), pero los circuitos electrónicos trabajan con frecuencias de señales senoidales que pueden llegar a cientos de millones de hertz.
Para generar formas de ondas senoidales o rectangulares no necesitamos tener obligatoriamente llaves o espirales cortando campos magnéticos. Los circuitos electrónicos pueden hacerlo fácilmente.
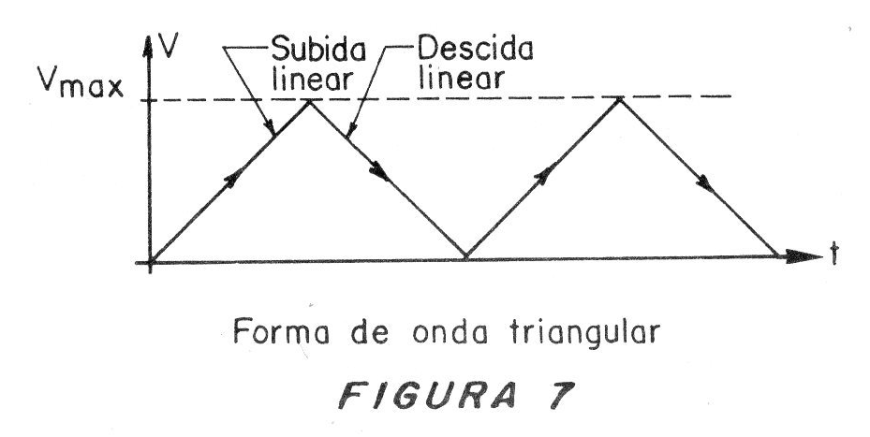
Finalmente, tenemos una tercera forma de onda que corresponde a variaciones de tensión que suben y bajan linealmente, como muestra la representación gráfica de la figura 7.
Esta forma de onda es denominada triangular, también por el hecho de su representación recordar la superposición de triángulos de diversos tipos.
Cuando aplicamos señales de formas de ondas diferentes en los circuitos, dependiendo de su naturaleza, no reaccionan de la misma manera. Cada tipo de señal tiene sus características propias en relación a un circuito, lo que hace que debamos escoger de modo apropiado cuál usar, cuando usamos, por ejemplo, un generador de funciones.
Lo que caracteriza cada tipo de señal será visto a continuación:
Señal senoidal
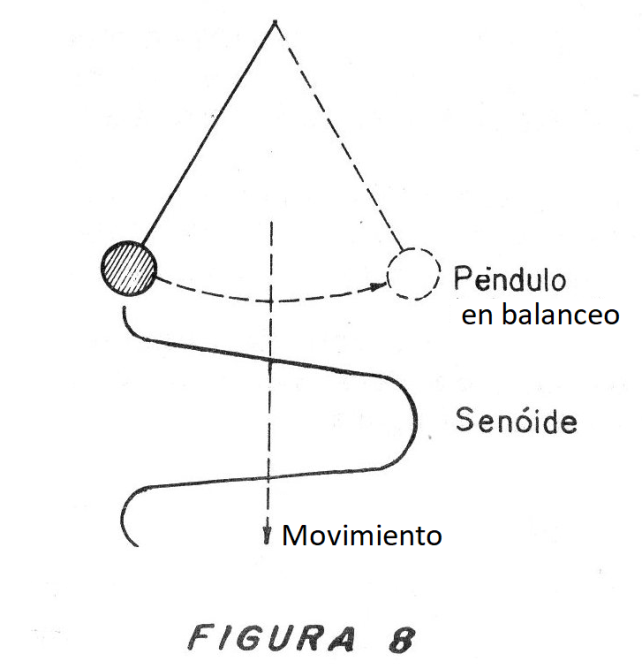
La señal senoidal corresponde a una oscilación pura, es decir, una oscilación que ocurre naturalmente. Si hacemos un cuerpo vibrar, un péndulo se balancea o un circuito electrónico formado por una bobina y un capacitor entra en oscilación, la representación de esta oscilación será un sinusoide, conforme la figura 8.
La senoide corresponde al tipo de oscilación que ocurre de la manera más suave posible, o sea, a la que tiende a ocurrir naturalmente. Los sonidos puros, tienen formas de ondas senoidales como, por ejemplo, el producido por un diapasón, usado en la afinación de instrumentos.
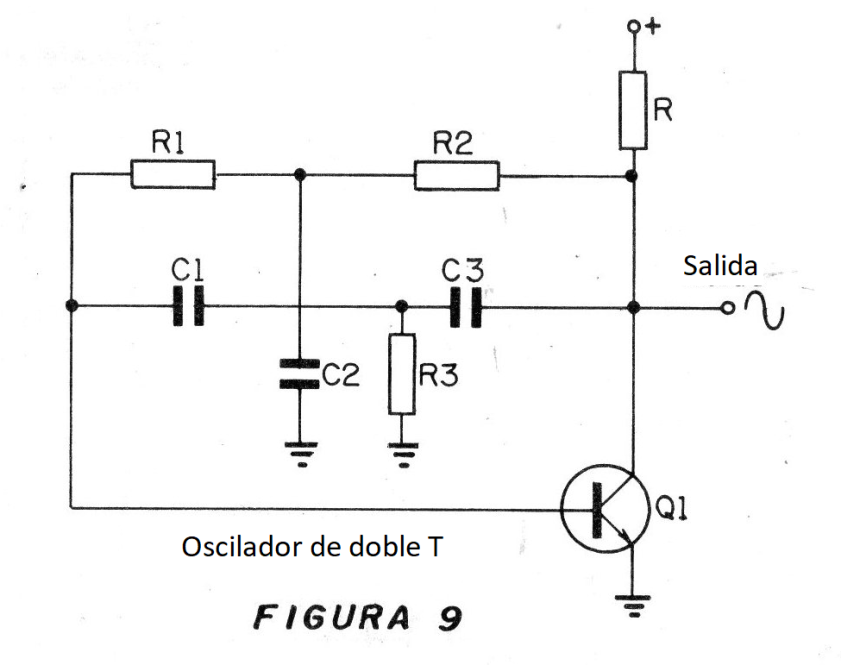
En la figura 9 damos un ejemplo de circuito electrónico que puede producir una señal senoidal.
Una característica importante de un signo senoidal puro es que está presente en una sola frecuencia, o sea, en la forma fundamental.
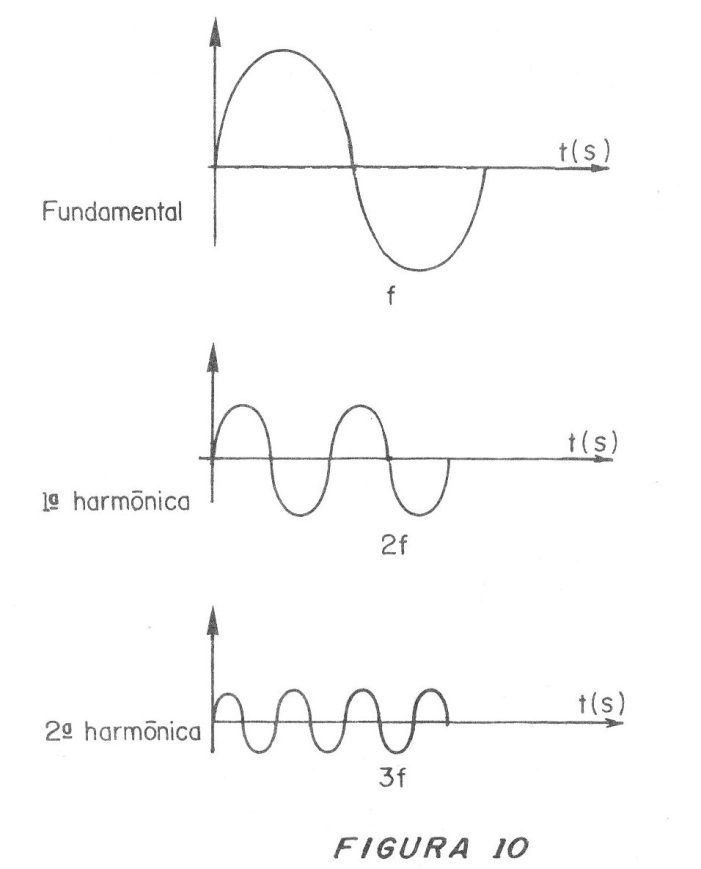
Lo que ocurre es que cuando se produce una señal no pura, frecuencias de valores múltiples también aparecen, como muestra la figura 10.
Estas frecuencias se denominan "armónicas" y corresponden al doble, al triple, al cuádruple de la frecuencia fundamental.
Cuando queremos trabajar con filtros, circuitos que deban operar en una sola frecuencia, la forma de onda utilizada es la senoidal.
Así, en la prueba de circuitos de este tipo debemos usar señales senoidales, lo mismo ocurre con un amplificador cuando queramos verificar su reproducción de una señal de una sola frecuencia.
Señal rectangular
Según Fourier, podemos producir cualquier tipo de señal a partir de la combinación en proporciones adecuadas de señales senoidales y sus armónicos.
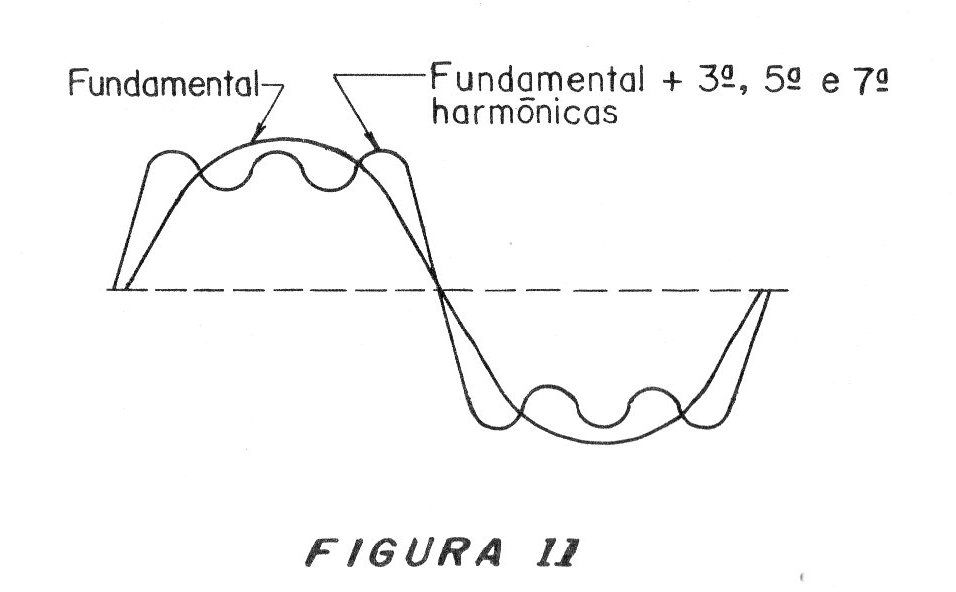
Así, una señal rectangular puede ser lograda por la superposición de un signo senoidal con diversas de sus armónicas, como sugiere la figura 11.
Tanto eso es válido que la recíproca es verdadera: una señal rectangular posee gran cantidad de armónicos que se extienden en una franja infinita de valores.
Así, una señal rectangular no es puro, sino compuesto de una gran cantidad de armónicos que cubren un espectro relativamente amplio. Intensidad relativa
En la práctica, por ejemplo, generando una señal rectangular de 1 kHz podemos tener tantos armónicos que su presencia se hará sensible incluso en frecuencias tan altas como 10 o 20 MHz.
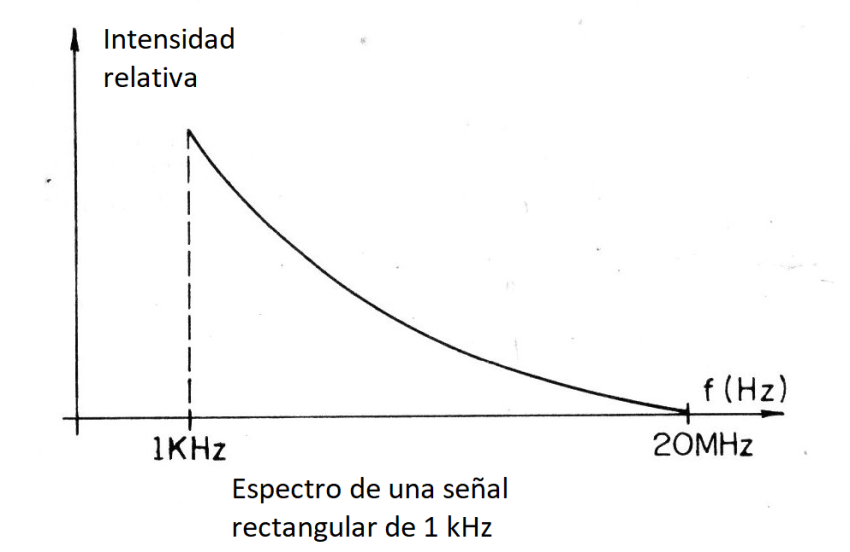
En la figura 12 tenemos una idea del espectro cubierto por una señal rectangular de 1 kHz.
Nota: en realidad esta curva está formada por pulsos que corresponden a los armónicos de una señal fundamental hasta 20 MHz.
Esta gran cantidad de armónicos es que hace que los circuitos de los inyectores de señales funcionen con formas de onda rectangulares en lugar de otro.
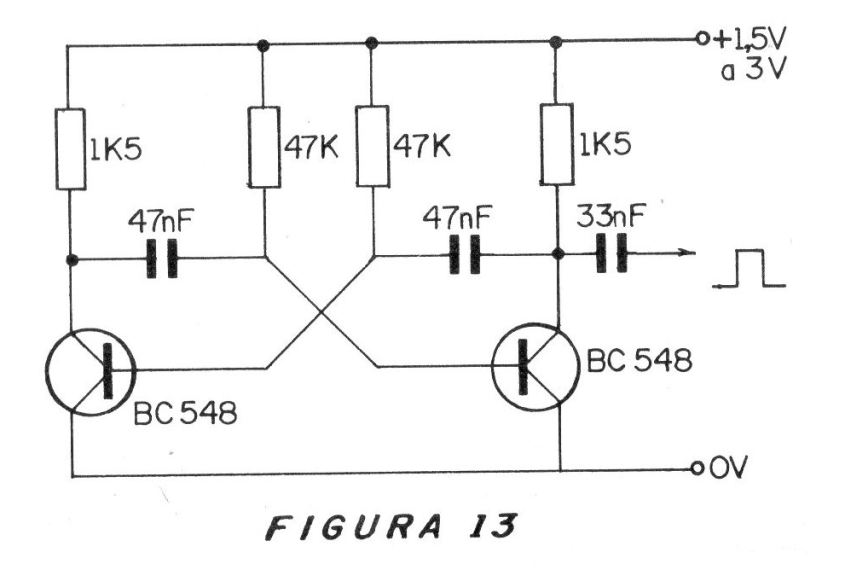
En la figura 13 tenemos un circuito de inyector de señales bastante simple que el lector puede montar para sus pruebas de banco.
Los transistores son de uso general (BC548 o equivalentes) y los resistores son de 1/8 o 1/4 de vatios, según su disponibilidad.
Los capacitores determinan la frecuencia fundamental de la señal producida que puede estar alrededor de 1 kHz para la mayoría de las aplicaciones prácticas.
En el caso de que se produzca un cambio en las condiciones de trabajo, se debe tener en cuenta que, en el caso de que se produzca un accidente,
Nuestro generador de señales se puede utilizar en forma de onda rectangular con el mismo propósito que un inyector.
Utilizaremos esta forma de onda para excitar circuitos de RF, con frecuencias muy por encima de los límites previstos para el oscilador. La presencia de gran cantidad de armónicos permite que hasta circuitos de FM sean analizados con el generador que fundamentalmente opere en una banda de audio.
Para utilizar el generador como inyector, es bastante simple: basta aplicar la señal en la entrada de la etapa que se desea analizar, siempre recordando que la intensidad de la señal para los armónicos decae a medida que su frecuencia aumenta. Así, si tenemos algunos volts en lo fundamental, en las armónicas las señales pueden tener sólo algunos milivolts o incluso microvolts.
Otra aplicación para las señales rectangulares es en la prueba de circuitos lógicos digitales.
Estos circuitos operan con dos niveles de tensión 0 y 5 V para los TTL y, O y Vcc donde Vcc es la tensión de alimentación, para los CMOS.
La velocidad de funcionamiento de estos circuitos puede superar los 10 MHz, lo que implica la producción o recepción de señales rectangulares de estas frecuencias.
Un generador de señales rectangulares puede, pues, ser utilizado para probar estos circuitos.
Sin embargo, para la utilización de un generador en estas condiciones es necesario que el nivel de señal de salida sea perfectamente conocido.
Si la señal está por debajo de cierto límite de valor, no habrá excitación del circuito en prueba y si es superior la tensión de alimentación se corre el riesgo de dañar el circuito en prueba.
La utilización de una señal rectangular en la prueba de amplificadores de. audio y. circuitos similares, exija la presencia de un osciloscopio.
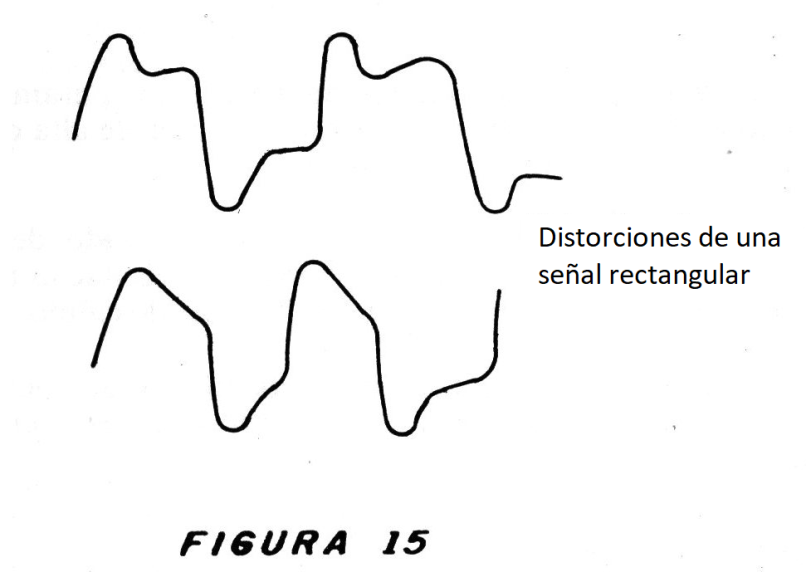
Deformaciones en forma de onda, como las mostradas en la figura 15, indican diversos tipos de problemas.
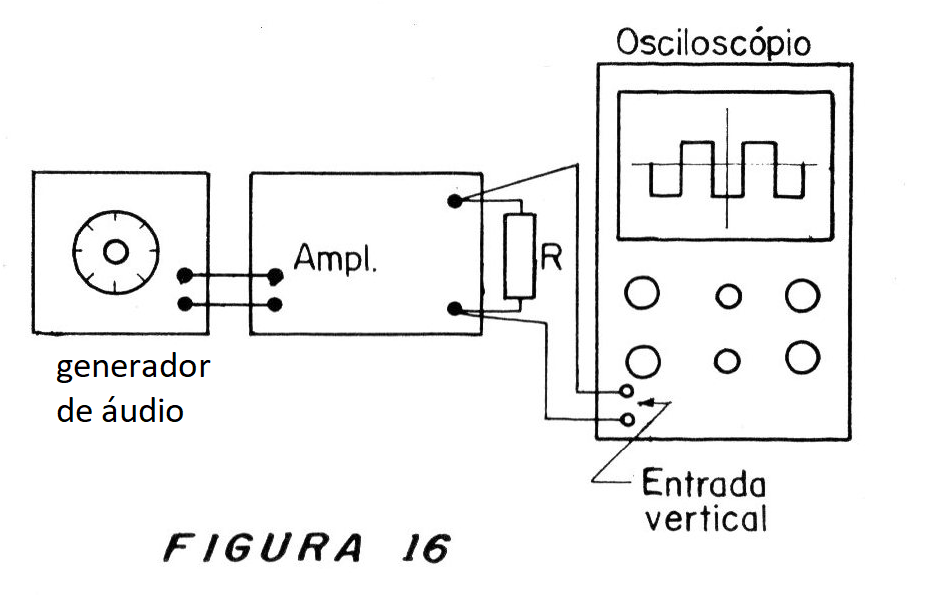
La conexión del generador y del osciloscopio se realiza como se muestra en la figura 16.
Observe que la carga del amplificador debe ser puramente resistiva siendo entonces el altavoz cambiado por un resistor de alta disipación (de acuerdo con la potencia del amplificador).
El nivel de señal de excitación debe ajustarse para tener excitación a plena potencia. El exceso de señal de excitación también puede provocar distorsiones que se verifican en el osciloscopio.
Es importante observar que la señal rectangular generada por un aparato ya puede estar dotada de cierta tasa de distorsión que debe ser previamente verificada.
Señales triangulares
Hasta hace algún tiempo había mucha controversia en cuanto al uso de señales triangulares en diversos tipos de pruebas de equipos electrónicos.
Tanto es así, que instrumentos de excelente calidad de algún tiempo atrás no disponían de señales con esta forma de onda
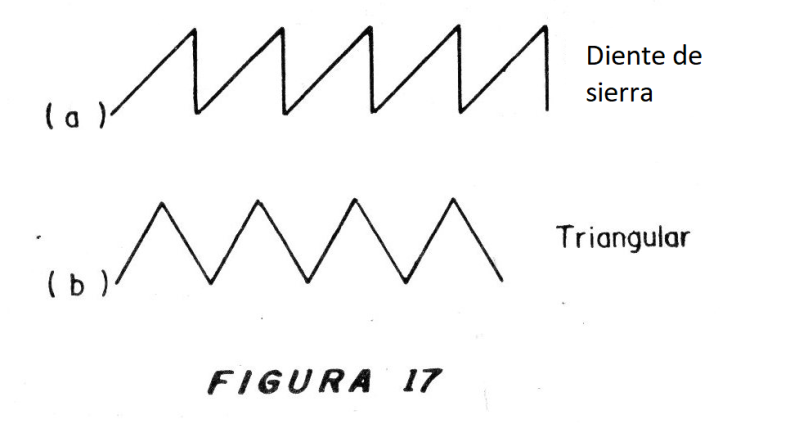
En la figura 17 tenemos un ejemplo de señal triangular generado por un instrumento de prueba común.
Nuevamente notamos que la forma triangular se refiere a la representación gráfica de las variaciones, nada teniendo que ver con el signo en sí.
Uno de los argumentos a favor de la utilización de señales triangulares en la prueba de equipos de audio se refiere a la mayor facilidad con que pueden detectarse las distorsiones.
Mientras que, con una señal senoidal, sólo se puede percibir una distorsión en un osciloscopio de al menos el 5%, utilizando una señal triangular, cualquier distorsión en torno al 2% ya puede ser percibida.
Esto significa que si pruebe un amplificador que presenta una distorsión, digamos del 3%, usando señal senoidal y el osciloscopio, usted no va a percibir nada. Sin embargo, probando el mismo amplificador con señal triangular, esta distorsión ya será fácilmente comprobada.
Otro factor que aparece a favor de la utilización de este tipo de señal es que los cambios de trazado de una forma de onda senoidal, verificados en un osciloscopio son de difícil interpretación.
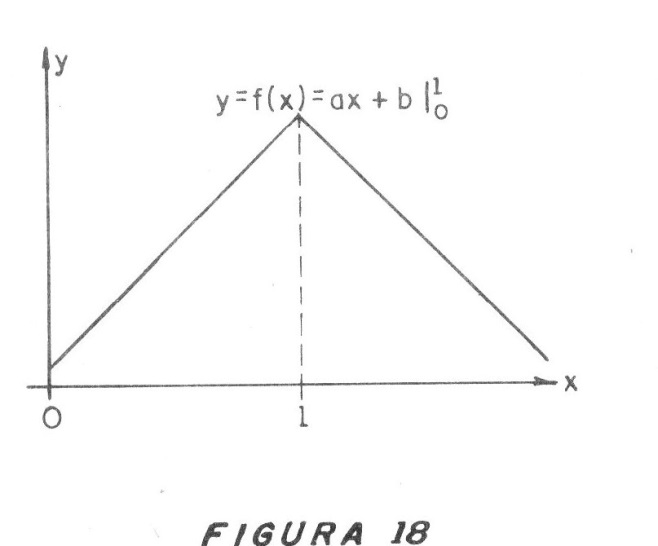
Se debe analizar una distorsión de función que sigue ley trigonométrica, lo que no ocurre con la señal triangular en que los tramos son funciones más simples, según leyes lineales, conforme a la figura 18.
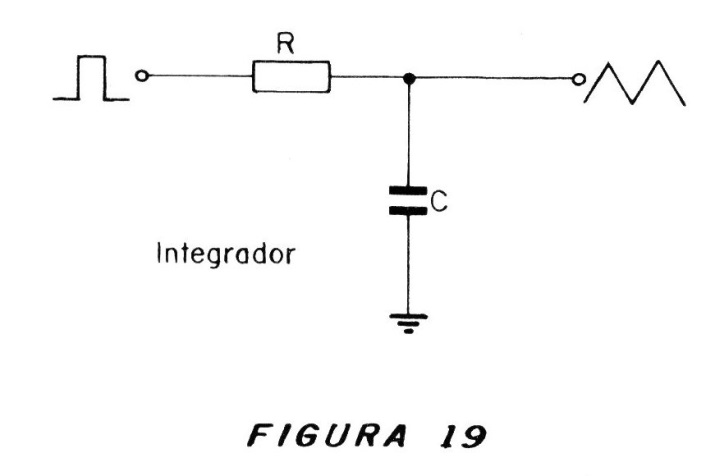
La producción de una señal triangular es relativamente simple a partir de una señal rectangular. Lo que se hace es usar un integrador, un circuito RC, como muestra la figura 19.
Los valores de R y C se calculan para producir los tramos lineales de la forma triangular de salida en las frecuencias de funcionamiento del circuito.
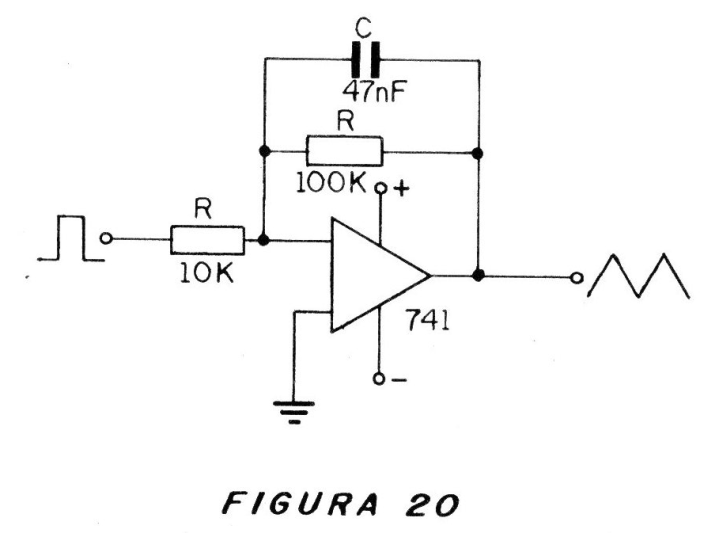
Un integrador más complejo, usando el amplificador operacional, se muestra en la figura 20.
En fin, las señales triangulares se pueden utilizar con los mismos propósitos.
En este artículo de un libro del autor publicado en los años 80. Sin embargo, por tratarse de tema teórico él es actual, pues los conceptos abordados son válidos en nuestros días.