6.1- Los Flip-Flops
El término flip-flop, báscula o multivibrador biestable está asociado a un tipo de circuito que, presentando sólo dos posibles estados, se convierte en compatible con algunas aplicaciones de secuenciación digital.
Por esta razón, los flip-flops consisten en dispositivos de gran importancia en la implementación de proyectos de electrónica digital, que merecen una lección completa aparte.
Estos circuitos se pueden utilizar para almacenar bits de información, para secuenciar la información digital y para hacer la división de frecuencia de las señales digitales, además de muchas otras funciones que quedarán claras a partir de ese momento, durante este curso.
Analicemos cómo funcionan los flip-flops o los multivibradores biestables.
Los flip-flops son elementos del circuito que pueden presentar en su operación solamente dos estados estables. No hay estados intermediarios entre estos dos estados.
Podemos compararlos con un balancín donde sólo hay dos posibles estados estables: cuando el lado A está en el nivel bajo o el lado B está en la parte superior y cuando el lado A está en la parte superior, el lado B está en el bajo. Las situaciones intermedias son inestables y no permanecen excepto durante las transiciones o cambios de estado, como se muestra en la figura 140.
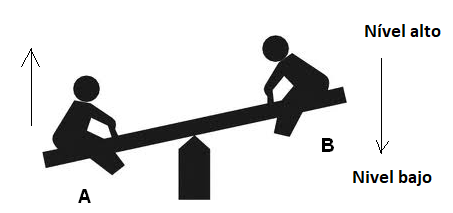
En el caso específico de un flip-flop electrónico, implementado con componentes como transistores, la aplicación de una señal de entrada puede causar un cambio de un estado a otro, y como en cualquier momento podemos saber en qué estado se encuentra, podemos Considere este circuito como una unidad de memoria capaz de almacenar un bit.;
Para esta capacidad de almacenamiento, el flip-flop se utiliza como un elemento básico de varios tipos de memorias.
Hay varios tipos de flip-flops que se pueden encontrar en los circuitos digitales.
Posteriormente, los flip-flops fueron implementados con los transistores discretos y el paso final en su evolución era su integración como elementos de los circuitos integrados de familias lógicas tales como TTL, CMOS o aún en memorias de varios tipos.
Para nosotros, en particular, es interesante conocer los principales tipos de flip-flops que se pueden encontrar en los circuitos integrados de las principales familias digitales, es sea, TTL y CMOS y lo vamos a analizar a partir de ahora.
6.2 - Flip-Flop R-S
El flip-flop R-S (de Reset y Set) – Este circuito tiene su configuración con transistores mostrados en la figura 141, funcionando de la siguiente manera:
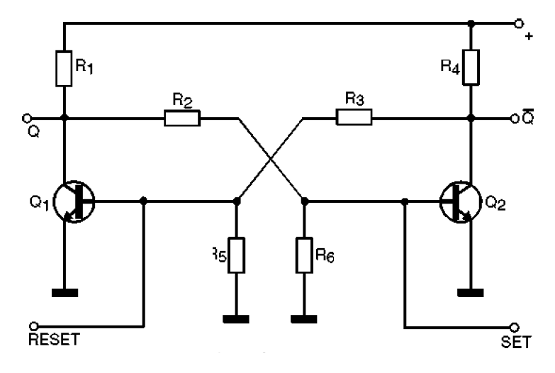
Cuando alimentamos el circuito, dadas las diferencias mínimas que pueden existir entre las características de los dos transistores, uno de ellos conducirá más que el otro. Suponiendo que este transistor es Q1 lo que ocurre es que hay una caída de tensión en su colector que reduce, como consecuencia, la corriente que polariza la base de la Q2 a través de R2.
En estas condiciones, la tensión del colector Q2 sigue siendo alta, realimentando la base del Q1 a través de R3 y se establece la situación final del circuito: Q1 satura y Q2 está en el corte. El flip-flop encuentra su estado estable inicial.
El flip-flop de R-S tiene dos salidas, representadas por Q y/Q, por lo que en la condición inicial estable con el primer Q1 Q será en el nivel bajo (0) y/q estará en el nivel alto (1).
El proceso que lleva el flip-flop a este estado inicial, listo para trabajar es muy rápido, no tarda más de unos pocos microsegundos, o incluso nanosegundos dependiendo de los componentes utilizados.
Cuando el flip-flop se encuentra en la situación indicada, con Q = 0 y /Q = 1 decimos que él se encuentra "setado" o aún fijo (el término "armado" también se puede utilizar).
El cambio de estado del flip-flop se puede lograr aplicando una señal en la entrada conveniente. A medida que usamos transistores NPN, para cambiar el flip-flop, tenemos que hacer que la unidad por un instante el transistor que se corta, o sea, debemos aplicar un pulso positivo en la entrada correspondiente.
Así, cuando el flip-flop está en la condición indicada y queremos cambiar el estado, aplicamos el pulso a la entrada SET. El transistor Q2 conduce por un instante, realimentando a través de R3 la base del Q1 que se corta. Con el corte, el tensión en la base del Q2 crece vía la polarización de R2, e incluso que el pulso del disparo desaparezca, el circuito permanece en el nuevo estado gracias a la realimentación.
Su salida Q va al nivel (1) y la salida /Q va al nivel (0).
Para cambiar el estado flip-flop de R-S de nuevo, aplicamos un pulso positivo en la entrada de RESET que lleva a Q1 a la saturación y Q2 al corte, situación que firme incluso después de que el pulso se ha perdido gracias a la retroalimentación proporcionada por los resistores.
Vea que un pulso aplicado a la entrada SET, que corresponde a un bit 1, causa la salida Q que estaba a 0 para pasar 1 por almacenar este bit. El flip-flop realmente funciona como un recuerdo para este bit.
Del mismo modo que usamos transistores bipolares NPN para conseguir un flip-flop, también podemos emplear otros tipos de componentes en configuraciones similares. Podemos, por ejemplo, elaborar flip-flop utilizando transistores PNP en cuyo caso se invertirá la polaridad de las señales de disparo.
Del mismo modo, podemos utilizar transistores de efecto de campo (FET), tanto de canal N como de canal P (bipolares o JFETs), así como transistores de efectos de campo MOS, con ambos tipos de canales (N o P). Lo que va a cambiar en cada caso es la dirección de circulación de las corrientes y las polaridades de las señales aplicadas.
Como hemos hablado, y vamos a ver en detalle en el último punto de esta lección, los flip-flops también se pueden hacer con válvulas y en realidad los primeros que existieron fueron correctamente montados con estos componentes. En aquel momento no había transistores (bipolares o FETs) o circuitos integrados.
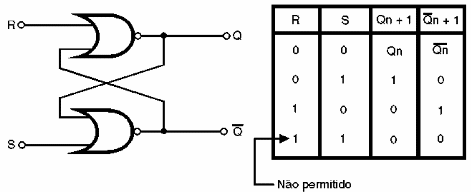
Los flip-flops se pueden fabricar con puertas lógicas y el R-S que estudiamos se puede obtener fácilmente a partir de dos puertas NAND de dos entradas, como se muestra en la figura 142.
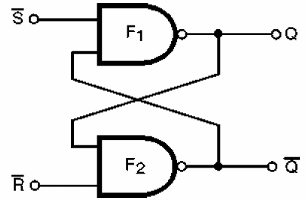
Teniendo en cuenta las tablas verdad de los puertas NAND, vemos que la salida de la primera puerta alimenta el segundo y viceversa, así garantizando el mantenimiento de los estados obtenidos cuando los interruptores del flip-flop.
Sin embargo, la conmutación de este circuito se produce cuando las entradas pasan del nivel alto al bajo, es sea, de 1 a 0. Esta condición se indica mediante los símbolos /R y /S de las entradas.
El lector puede entonces darse cuenta que cuando las entradas son ambas en el nivel bajo, el flip-flop permanece en el estado en el cual fue puesto encendido o por una conmutación anterior.
Por otra parte, si las entradas se toman simultáneamente en el alto nivel, el flip-flop va a un estado indeterminado que debe ser evitado. En la práctica, la aplicación de niveles altos (1) en ambas entradas puede destruir el dispositivo.
El diagrama de tiempo en la figura 143 muestra lo que ocurre en la operación por etapas de un flip-flop y que puede ser analizado de la siguiente manera.
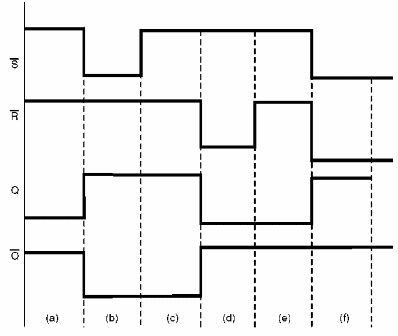
En la figura tenemos las siguientes condiciones del flip-flop a considerar:
a) Flip-flop reseteado
b) /S va al nivel bajo y el flip-flop es setado
c) /S va al nivel alto y el flip-flop sigue setado
d) /R va a nivel bajo y el flip-flop permanece reseteado
e) /R vuelve al nivel alto y el flip-flop sigue siendo reseteado
Todo esto puede ser representado por una tabla verdadera, tal como lo hacemos con las funciones lógicas. En esta tabla tenemos algunos símbolos nuevos con los que el lector debe empezar a familiarizarse y que son ampliamente utilizados en la electrónica digital, a saber:
a) Primera posibilidad
Qn-1 = representa el estado de la salida Q ANTES de que se apliquen las señales.
Qn = representa el estado de la salida de Q DESPUÉS de la aplicación de las señales.
b) Segunda posibilidad
Q = representa el estado de la salida Q ANTES de que se apliquen las señales.
Qn + 1 = representa el estado de la salida Q DESPUÉS de que las señales son aplicadas.
Se utilizan los dos tipos de representación.
En las columnas y líneas donde se colocan los niveles lógicos 0 y 1, cuando aparece el término Qn o/Qn, esto indica que la salida va a un estado indeterminado.
La tabla verdadera del flip-flop de R-S con los puertas del NAND es entonces:
| R | R | Qn | /Qn+1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | Qn | /Qn |
Para conseguir un flip-flop de R-S podemos también utilizar los puertas, como se muestra en la figura 144.
En la figura 145 tenemos los símbolos adoptados para representar este tipo de flip-flop.
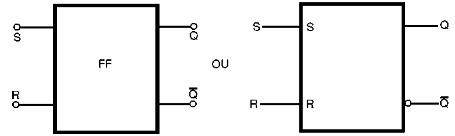
Este circuito también es llamado R-S NOR LATCH, al igual que el circuito anterior se llama R-S NAND LATCH.
La palabra "LATCH" significa bloqueo o traba, lo que sugiere que es un circuito que "bloquea" en cierta posición de los comandos R y S y utiliza los puertas NAND o NOR. El término LATCH en inglés puede por lo tanto también estar asociado con flip-flops.
6.2.1 – Repiques
Cuando cerramos un interruptor, o incluso unos sensores accionados, el establecimiento de corriente en el circuito no es inmediato. Los contactos mecánicos tienden a oscilar, causando así diversos pulsos de variación de la tensión o de la corriente, llamados repiques, o usando el término inglés
"bounce" (balance),
Estos repiques hacen que el circuito digital que debe recibir el mando del interruptor o sensor interprete la señal de entrada como más de un pulso, como se muestra en la figura 146.

En este caso, el cierre del sensor se interpreta como una secuencia de tres pulsos. Si el circuito tiene que contar pulsos, el contaje será 3, no sólo un candado.
6.3 – Flip-flops RS con el Clock Maestro-Esclavo
Este circuito, llamado el flip-flop de R-S controlado por el clock (*) y el maestro esclavo, encuentra una gama de aplicaciones muy grande en los circuitos digitales más complejos, puesto que se comandan siempre por un clock, es sea son circuitos lógicos sincronizados.
El uso de un circuito de control (maestro) que determina cuándo cambia el estado del flip-flop (esclavo) es importante para permitir que los cambios del estado del flip-flop ocurran solamente en instantes bien determinados.
Utilizando las puertas NAND podemos implementar inicialmente un flip-flop de R-S controlado por clock (Master-Slave) como se muestra en la figura 147.
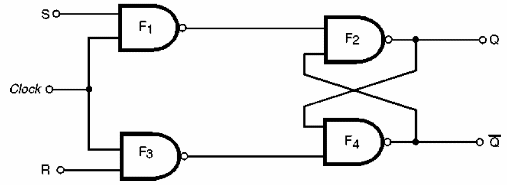
Analicemos su funcionamiento:
A partir de la situación en la que la entrada del clock (reloj) se encuentra a un nivel bajo, las salidas Q y/Q permanecerán en el estado inicial en el que se encuentran e insensibles a cualquier variación ocurrida en las entradas S y R (Set y RESET).
Cuando la entrada del clock se lleva al nivel 1, el circuito comienza a responder a las señales de las entradas R y S.
Sin embargo, como se muestra en el diagrama de tiempo de la figura 148, este circuito tiene un inconveniente.
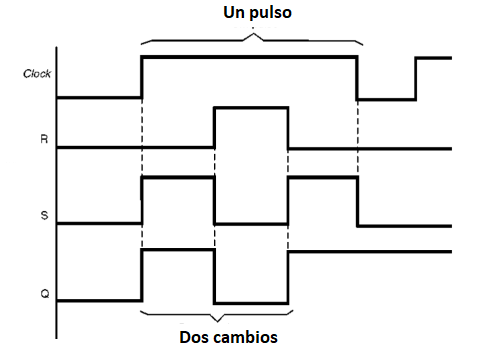
Como las salidas acompañan a las entradas, durante el tiempo en que el clock los habilita, estas salidas pueden cambiar de estado más de una vez, volviendo al estado inicial, que no se desea de ninguna manera, ya que conduciría el circuito a una inestabilidad de funcionamiento.
Una forma de solucionar este problema es utilizar dos pasos en una configuración más compleja, que se muestra en la figura 149.
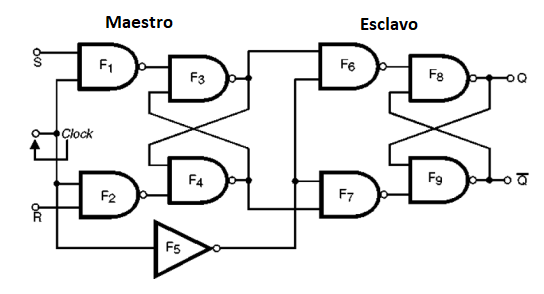
Se obtiene entonces una configuración más elaborada en la que se aísla el paso de salida que el flip-flop propiamente dicho y la etapa de control, en la que tenemos los comandos set y reset.
Este circuito se llama Flip-Flop R-S Maestro-Esclavo o Flip-Flop R-S Master-Slave pudiendo hacer uso de ambos puertas NAND y un inversor cuyo propósito es invertir el pulso del clock (F5).
Al aislar los dos pasos, los cambios de señal que ocurren en el primer paso no afectan al segundo paso, excepto cuando esto es necesario.
Lo que ocurre en este caso es que cuando la entrada del clock está en el nivel 1, el flip-flop maestro cambiará de estado, pero el flip-flop esclavo seguirá siendo insensible, manteniendo su estado.
Cuando la entrada del clock pasa al nivel lógico 0, la salida del flip-flop maestro será llevada al esclavo.
Esto significa que el flip-flop, en su conjunto, no es sensible al nivel de la señal del clock, es sea, si es 0 o 1, sino más bien a su transición. Las salidas Q y /Q sólo cambiará de estado en el momento en que ocurra la transición, desde la señal de clock de alto nivel hasta el nivel bajo.
Con esta configuración es posible asegurar que sólo un cambio de estado ocurrirá en presencia de un pulso de clock.
Los flip-flops que funcionan de esta manera se llaman "Edge Triggered" o "disparados por el Borde", refiriéndose al pulso de disparo.
El término "Borde" se refiere a la transición de una señal, es sea, al tramo de la curva que representa la tensión en la que varía entre el nivel 0 y 1 (borde de ascenso), o del nivel 1 al 0 (borde de descenso). También es común utilizar el término “frente" para indicar estas variaciones.
Así, también llamamos "frente positivo" al pasaje en el que se produce la variación de la señal de 0 a 1 y una fuente negativa al extracto que tenemos la variación de 1 a 0.
Si el cambio de estado o disparo (gatillo) ocurre cuando la señal del clock va de 0 a 1, los flip-flops se llaman "positive edge-triggered" (accionado por el borde o la frente positiva), mientras que el disparo ocurre cuando el clock pasa de nivel 1 a 0 , esto es, en la caída del nivel lógico, los flip-flops se llaman "negative edge-triggered" (accionado por el borde o la frente negativa).
La mayoría de los flip-flops de este tipo disponible en forma de circuito integrado es el tipo desencadenado por la transición negativa de la señal del clock.
En la figura 150 tenemos una representación más común para este tipo de flip-flop, en el que tenemos los circuitos internos, en caso de que la señal del clock se aplique directamente al flip-flop maestro (M).
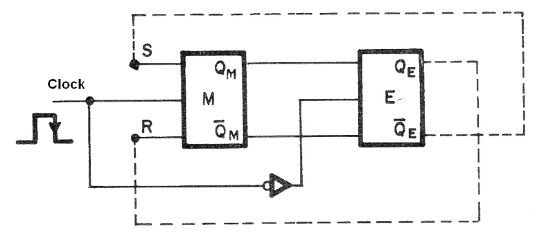
Sin embargo, en la simbología más usual, tenemos la representación mostrada en la figura 151 en la que sólo tomamos en cuenta las entradas y salidas.
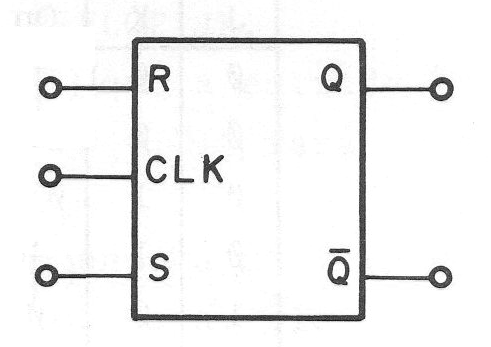
Cuando este tipo de flip-flop se utiliza en un proyecto de mayor velocidad, es muy importante tener en cuenta los tiempos en que se produce todo el proceso.
Así, a partir del diagrama de tiempo de la figura 152, vemos que la salida del flip-flop sólo completa su cambio de estado después de cierto tiempo, desde el instante en que se aplicó el pulso del clock.
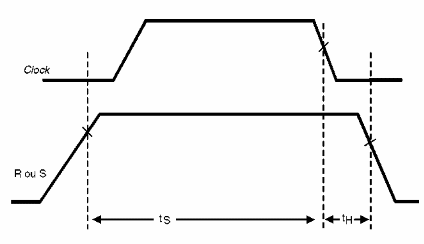
Dos tiempos son importantes en este tipo de circuito.
a) th llamado de Hold Time o Tiempo de Mantenimiento y es el tiempo en que la entrada debe permanecer todavía en el circuito para que su nivel lógico sea reconocido por el flip-flop.
b) ts es llamado tiempo de Setup Time o tiempo de sujeción y es el momento en que la entrada del flip-flop debe permanecer en el estado deseado, antes de la transición del clock que causará el cambio de estado del circuito.
Se pueden añadir dos entradas a este circuito, como se muestra en la figura 153, dándole importantes recursos para aplicaciones prácticas.
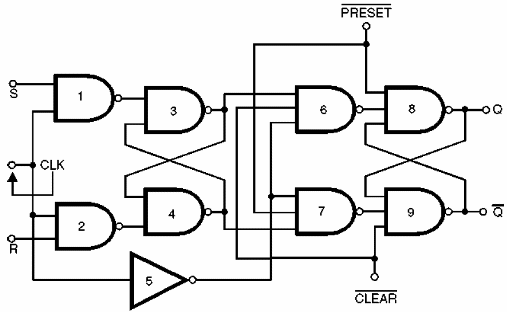
Una de las entradas se llama PRESET (/PR), o pre ajuste, y tiene la función de tomar inmediatamente las salidas del circuito a un estado dado (Q = 1 y /Q = 0) independientemente de lo que pueda estar sucediendo en las otras entradas.
Su activación se produce cuando/PR está en 0 y /CLR a 1, en el caso indicado, pues a / sobre la identificación indica que ella está activo en el nivel bajo.
La otra entrada llamada CLEAR, o borrador, tiene la función de tomar las salidas a los estados Q=0 y /Q=1 independientemente de lo que ocurra en las otras entradas.
En la figura 154 tenemos la representación común para este tipo de flip-flop.
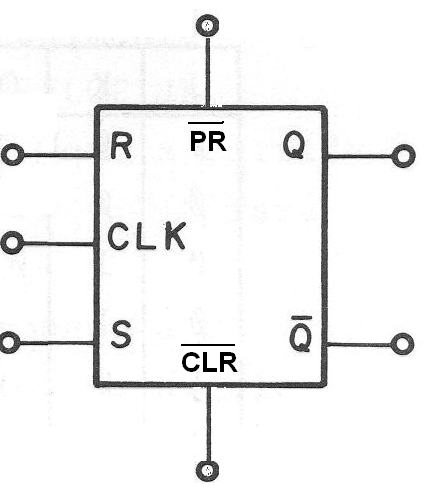
Es importante notar que estas dos entradas no pueden ser activadas al mismo tiempo, ya que esto llevaría al circuito a un estado indeterminado que podría incluso causar problemas a sus componentes.
Ya hemos advertido que es común que en funciones más complejas, como los flip-flops, haya "situaciones prohibidas". Hay combinaciones de niveles lógicos que no pueden estar presentes al mismo tiempo en ciertos insumos, ya que pueden llevar el circuito a un estado indefinido, es sea, donde no es posible predecir, que ocurrirá con la salida. Un ejemplo simple es el que aplicamos al mismo tiempo niveles de disparo en las entradas Set y Reset de un flip-flop al mismo tiempo.
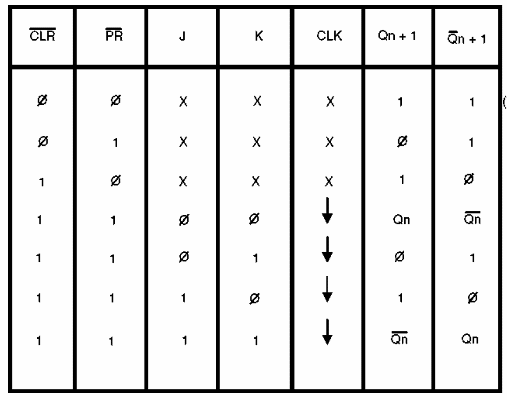
Volviendo a nuestro ejemplo, la tabla verdadera para este circuito nos muestra tres nuevos símbolos que se utilizan habitualmente en la electrónica digital.
X representa una condición irrelevante, es sea, sea lo que sea, no habrá influencia en lo que ocurra en la salida.
La flecha ascendente indica la transición de bajo nivel al nivel de señal en la entrada o salida representada mientras que la flecha hacia abajo indica una transición de alto nivel al alto nivel de la señal correspondiente.
|
/CLR |
/PR |
R |
S |
CLK |
Qn+1 |
/Qn+1 |
|
0 |
0 |
x |
x |
x |
1 |
1 |
|
0 |
1 |
x |
x |
x |
0 |
1 |
|
1 |
0 |
x |
x |
x |
1 |
0 |
|
1 |
1 |
0 |
0 |
↓ |
Qn |
/Qn |
|
1 |
1 |
0 |
1 |
↓ |
1 |
0 |
|
1 |
1 |
1 |
0 |
↓ |
0 |
1 |
|
1 |
1 |
1 |
1 |
↓ |
1 |
1 |
↓ - no importa
Qn y /Qn – no cambia
6.4 – El flip-flop J-K Maestro-Esclavo
Incluso usando dos pasos, el flip-flop que vimos todavía puede presentar algunos problemas de funcionamiento cuando se utiliza en ciertas aplicaciones.
Una mejora de este circuito es que veremos a continuación.
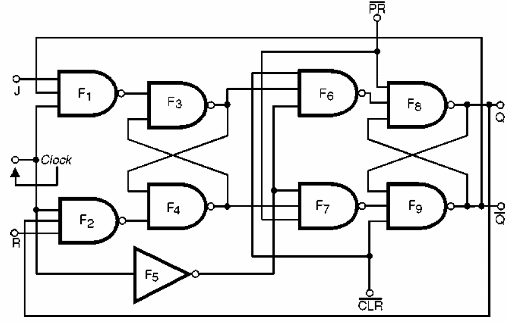
El flip-flop J-K maestro-esclavo o “master-slave”, al igual que las otras funciones que estudiamos, puede ser implementado por funciones lógicas comunes mediante la adquisición de la configuración básica que se muestra en la figura 155.
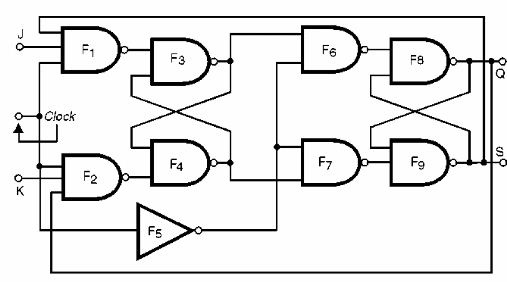
Un problema que observamos en los flip-flop de R-S es que tenemos una situación "prohibida" que ocurre cuando las entradas R y S van al nivel alto al mismo tiempo, lo que puede llevar el circuito a un estado indeterminado, como ya hemos advertido.
Esta situación se produce principalmente en las aplicaciones en computación y control cuando se utiliza una parte de la señal de salida para realimentar la entrada. En estas condiciones, pueden ocurrir situaciones de conflicto, con la producción de oscilaciones no deseadas e incluso resultados imprevisibles en los circuitos que deben ser excitados.
Esta situación se puede contornar con el uso de una nueva configuración que es precisamente la del flip-flop J-K, y vamos a analizar a continuación. Esta configuración, por sus ventajas en ciertos circuitos, es la más utilizada en aplicaciones prácticas.
Luego dejamos las entradas de este tipo de flip-flop. Podemos tener cuatro combinaciones posibles para las señales aplicadas en las entradas J y K, como se muestra en la tabla de abajo.
J K
0 0
1 0
0 1
1 1
Analicemos cada uno de ellos:
a) J = 0 y K = 0
Cuando la entrada del clock (CLK) pasa por una transición negativa, la señal del flip-flop conserva su condición original que no cambia de estado.
b) J = 1 y K = 0
Cuando la entrada del clock (CLK) pasa por una transición negativa, el flip-flop es "setado". Si ya está setado permanece en esta condición.
c) J = 0 y K = 1
Cuando la entrada del clock (CLK) pasa por una transición negativa, el flip-flop es "reseteado". Si ya está en esta condición permanece.
d) J = 1 y K = 1
En esta condición, al recibir una transición negativa en la entrada del clock (CLK), el flip-flop cambia de estado (TOGGLE) (*). Si estuviera setado él resetea y si estuviera se reseteado él es setado.
Podemos elaborar la tabla verdad de la figura 156 para indicar lo que sucede con este flip-flop.
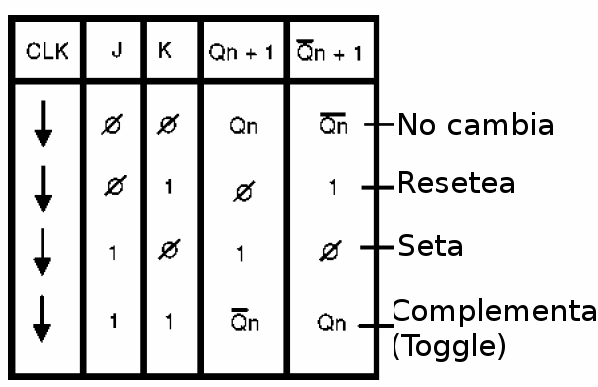
Note el uso de las flechas para indicar las transiciones de la señal en la entrada del clock, que ordenan el funcionamiento de este tipo de circuito.
Como en las otras configuraciones que estudiamos, también podemos incluir las entradas PRESET y CLEAR en este circuito, que se mostrarán en la figura 157.
A continuación, se muestra una tabla verdadera que incluye las entradas PRESET (PR) y CLEAR (CLR) es mostrada abajo.
Una mejor manera de analizar el funcionamiento de este circuito es a través de un diagrama de tiempo, en el cual observamos las formas de onda en los distintos puntos de entrada y salida. Este diagrama de tiempo para el flip-flop J-K se muestra en la figura 158.
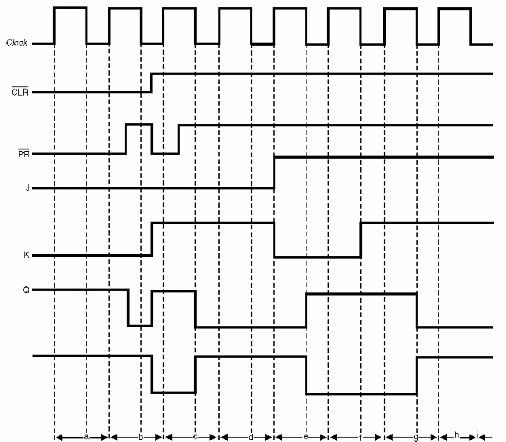
Analicemos algunos extractos importantes de este diagrama. Mostrando lo que sucede:
a) En este instante, CLR y PR están en el nivel bajo, Q y/Q están en el nivel alto, que es una condición desautorizada.
b) A continuación, se aplica la señal PR que, yendo al alto nivel, hace que el flip-flop sea reseteado.
c) La aplicación de un pulso en la entrada de CLR que va al nivel alto, y el viaje PR al nivel bajo, ahora hace que el flip-flop sea setado.
d) CLR y PR se mantienen en el alto nivel desde este instante. Con J = 0 en este fragmento y K yendo al alto nivel, el flip-flop será reseteado en la siguiente transición negativa de la señal del clock.
e) Aún con CLR y PR en el alto nivel (esta condición se mantendrá en adelante), y la salida J = 0 y k = 1, el flip-flop sigue siendo reseteado.
f) Con J = 1 y K = 0, el flip-flop se establece en la próxima transición del pulso del clock.
j) Con J = 1 y K = 0 no se producen cambios de estado.
h) Con J = 1 y K = 1 en la transición siguiente del pulso del clock el flip-flop cambia el estado (complementa o "Toggle"). Si estuviera reseteado, como en este caso, él es setado.
i) Manteniendo J= 1 y K = 1 con nueva transición del pulso de clock, el flip-flop cambia de estado otra vez, o sea, complementa.
Vea que cuando las entradas J y K están en el nivel alto, el circuito se compone como un disparador, cambiando de estado a cada transición negativa del pulso del clock.
Como el lector verá en las lecciones futuras, en la mayoría de las aplicaciones digitales, la operación es dinámica, con los niveles de entrada y salida de las diversas funciones que cambian constantemente. Esto significa que en muchas aplicaciones, el análisis del circuito no se limita a saber qué ocurre con una salida cuando ciertas entradas tienen ciertos niveles.
Puede ser necesario analizar la dinámica del funcionamiento del circuito y, en este caso, los diagramas de tiempo son mucho más apropiados.
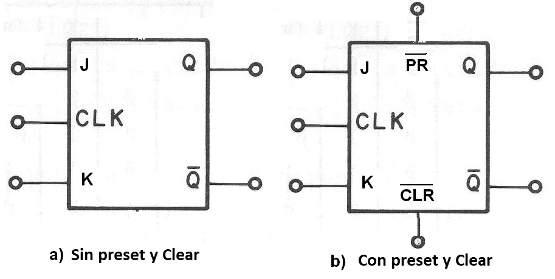
El símbolo usual para este tipo de flip-flop se muestra en la figura 159.
6.5 - El flip-flop tipo D
Los flip-flops tipo D también encuentran una amplia gama de aplicaciones prácticas. En la figura 160 tenemos el símbolo adoptado para representar este tipo de flip-flop.
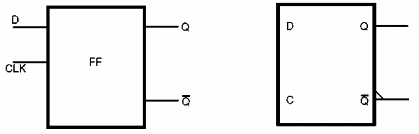
El flip-flop de tipo D tiene una sola entrada que ejecuta toda su operación. Esta entrada le da un nombre. Llamado "Data" (dados), es abreviado por D y de ahí el nombre del dispositivo.
Este flip-flop funciona de una manera muy simple: en la pulso del clock se asume el estado de la entrada, como podemos ver en su tabla verdad:
D Qn+1
0 0
1 1
Por su simplicidad de operación funcionan muy bien las aplicaciones como divisores de frecuencia, contadores de pulsos, etc.
6.6 – Flip-flop tipo T
El nombre de este flip-flop proviene de "Toggle" (T) o complementación, y su símbolo se muestra en la figura 161.
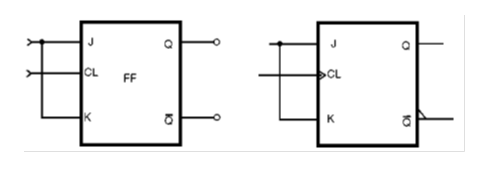
Lo que hace este circuito se puede entender fácilmente por el diagrama de tiempo mostrado en la figura 162.
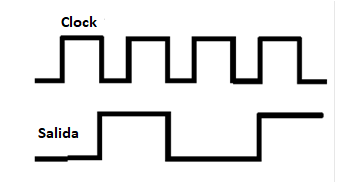
Cuando la entrada T de este circuito está a bajo nivel, el flip-flop permanece en su estado anterior, incluso con la aplicación del pulso del clock. Sin embargo, cuando la entrada T está en el nivel alto, el flip-flop cambia de estado. Si estaba setado él resetea, y si estaba reseteado, la seta
Este comportamiento realmente significa dividir la frecuencia del clock por dos. En otras palabras, este circuito se compone como un divisor de frecuencia, encontrando aplicaciones prácticas muy importantes en la electrónica digital.
Un ejemplo de aplicación se da en la figura 163 en la que se asocian varios flip-flops de tipo T en serie para que, pasando a través de cada una la frecuencia de la señal de entrada, tenemos su división por 2.
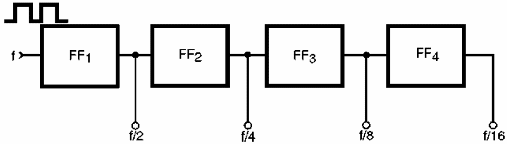
Usando 4 flip-flops, podemos dividir la frecuencia de una señal de entrada por valores que son potencias de 2, tales como: 2, 4, 8 y 16.
Este tipo de divisor de frecuencia es ampliamente utilizado, hasta el punto de que hay circuitos integrados que tienen secuencias de más de 10 flip-flops conectados de esta manera.
En la práctica no tenemos los flip-flops tipo T como componentes listos para utilizar. Lo que usted puede hacer es conseguir este flip-flop de otros y esto se verá en el siguiente elemento.
6.7 – Transformando Flip-Flops
De la misma manera podemos obtener cualquier función lógica compleja de funciones sencillas, que se vio en las lecciones anteriores, también podemos "jugar" con los flip-flops, obteniendo otros tipos de un tipo básico.
Por lo tanto, usando un flip-flop R-S o J-K, que son comunes, y algunos puertas lógicos, podemos conseguir flip-flops de otros tipos.
En la figura 164 tenemos algunas conversiones que se pueden hacer usando flip-flops de tipo R-S.
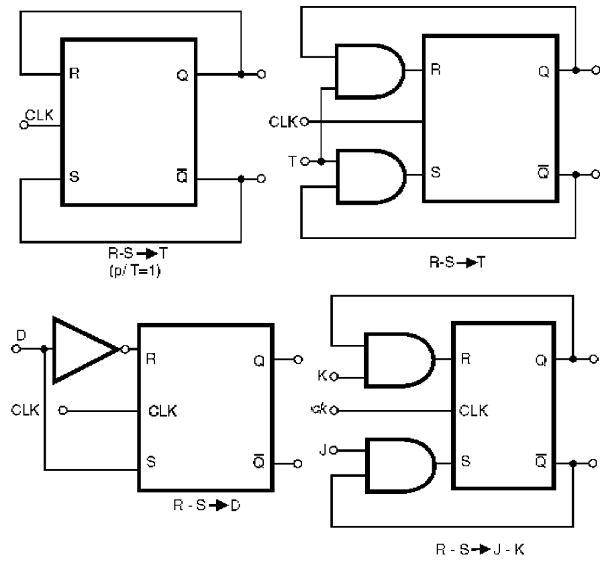
El modo de operación de cada uno se puede entender fácilmente si el lector intenta asociar las tablas verdadera de los flip-flops que fueron estudiadas en esta lección a las tablas verdadera de los puertas agregados, considerando las señales de la realimentación.
Por lo tanto, empezamos con la figura 165, donde tenemos el modo de conseguir flip-flops tipo D y T de flip-flops de tipo J-K.
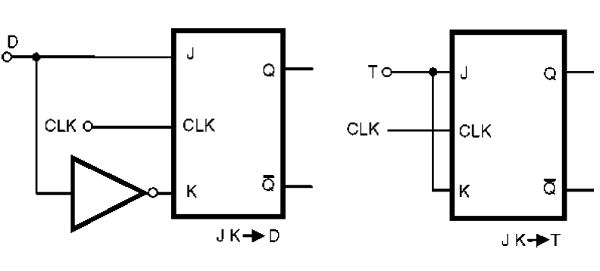
Vea que la conexión simple de la entrada de K al J en el flip-flop del tipo J-K lo convierte en un flip-flop tipo T. Esta posibilidad es muy interesante, puesto que los flip-flops J-K están disponibles en la tecnología de la TTL como CMOS y se pueden utilizar en circuitos de los divisores de frecuencia.
Cuando hablamos de los tipos específicos de circuito integrado de flip-flops de las familias TTL y CMOS, el lector tendrá información sobre varios tipos de flip-flops que se pueden utilizar en proyectos prácticos.
De hecho, ya hemos utilizado esta configuración en varios de nuestros proyectos prácticos publicados en libros, revistas y en nuestro sitio Web.
Finalmente tenemos otras dos transformaciones importantes de flip-flops que se muestran en la figura 166.
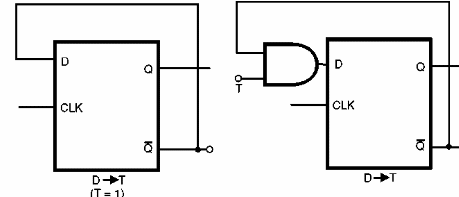
En el primer caso tenemos una transformación un flip-flop tipo D en el flip-flop tipo T, sólo para que la salida complementar /Q esté conectada a la entrada D, realimentando el circuito.
La segunda transformación, que toma un flip-flop tipo D para funcionar como tipo T, requiere el uso de un puerto AND adicional en la retroalimentación de la señal que se toma de la salida complementar /Q.
Vea que es muy importante saber cómo transformar flip-flops, así como las funciones lógicas. Muchos circuitos integrados tienen más de un flip-flop disponible en la misma cubierta. Por lo tanto, si necesitamos un flip-flop tipo D y un tipo T, podemos utilizar un circuito que tiene dos del tipo D y se convierte en uno de ellos y un tipo T.
El resultado es que, con un solo componente, obtenemos las dos funciones, con ahorro de gastos y espacio en la tarjeta de circuitos impresos.
6.8 – En los equipos digitales
Encontramos los flip-flops en computadoras, equipos de telecomunicaciones, controles industriales, equipos electrónicos embebidos, robots y muchos otros, como elementos fundamentales de muchos circuitos.
Uno de los usos más importantes del flip-flop está en la división de la frecuencia de clock. Como sabe el lector, hay sectores de un equipo digital que deben operar a velocidades inferiores a las proporcionadas por el clock principal.
Este es el caso de micro controladores y microprocesadores y varios controles en los que se conectan la expansión, tarjetas de adquisición y control de datos, módems, salidas de datos de los puertas paralelos y serie, etc.
Así, en lugar de utilizar un clock para cada frecuencia deseada, lo que se hace es emplear un clock único y dividir su frecuencia de acuerdo con los requisitos de frecuencias bajas, como se muestra en la figura 167.
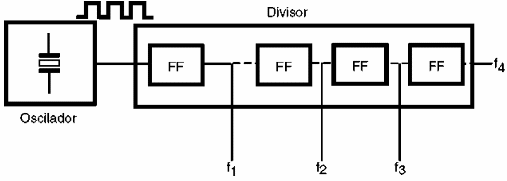
En el caso de muchos equipos digitales, tanto el clock como la secuencia de los divisores flip-flops divisores se pueden obtener en un único circuito integrado.
Un punto importante que debe tenerse en cuenta, y que vamos a estudiar en las lecciones futuras, es que podemos conectar los flip-flops junto con otras funciones, de modo que la frecuencia puede ser dividida por cualquier número, y no sólo por los poderes de 2 como 2, 4, 8, 16, 32, 64, 128, etc. Como eso es hecho, serán estudiados más adelante.
Otra aplicación importante es como la célula de memoria. Ocho flip-flops vinculados de lado a lado pueden almacenar un byte entero. Cada flip-flop almacena un bit.
Hay varias memorias internas, utilizadas en equipos digitales que nada más que flip-flops dispuestos en matrices, que contienen gran cantidad de ellos, y que se puede habilitar tanto para la lectura de datos como para la introducción (grabación de datos).
Todavía hay muchas otras funciones importantes que pueden ser implementadas desde flip-flops y serán estudiadas en las siguientes lecciones.
6.9. Los flip-flops antiguos
La configuración flip-flop no es nueva. Realmente fue en 1919 que dos investigadores norteamericanos llamados Eccles y Jordán presentaron el primer circuito flip-flop usando válvulas, como se muestra en la figura 168.
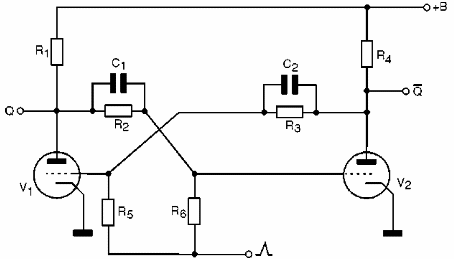
Por esta razón, muchos profesionales de la "vieja-escuela" todavía llaman los flip-flops de "Basculas o Circuitos Eccles-Jordán" cuando se refiere a esta configuración.
En 1930, los físicos ya utilizaron estos circuitos conectados en serie para dividir el contaje de los pulsos de contadores Geiger de radiación con el fin de obtener valores más pequeños más fácilmente totalizados en las pesquisas.
Un contador binario usando una lámpara de neón conectada a las válvulas fue desarrollado usando estos flip-flops ya en 1940, pero era solamente después de este tiempo que las primeras computadoras digitales comenzaron a utilizar estos circuitos de una manera más intensa, hasta la llegada del transistor y después de los circuitos integrados.
Sumário
Curso de Electrónica - Electrónica Digital (CUR5000)
Curso de Electrónica - Electrónica Digital – Parte 1 (CUR5001S)
Curso de Electrónica Digital – Parte 2 - El Álgebra de Boole (CUR5002S)
Curso de Electrónica - Electrónica Digital - Parte 6 - Los Elementos Biestables (CUR5006S)
Curso de Electrónica - Electrónica Digital - Parte 9 - Contadores Digitales (CUR6002S)
Curso de Electrónica - Electrónica Digital - Parte 13 - Memorias, ADCs y DACs (CUR6006S)




