13.1 – Las memorias
El almacenamiento de información es fundamental para el funcionamiento de ordenadores, cámaras digitales, instrumentos de medición, automatismos y también varios otros aparatos electrónicos.
Sin embargo, la información disponible en un circuito se presenta de una manera especial, en forma de tensiones o impulsos, y esto hace que también requiera dispositivos especiales para su almacenamiento.
13.1.2 – Bits y Bytes
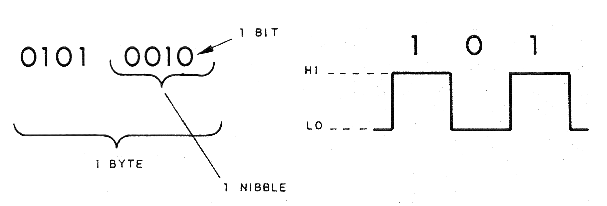
Como saben los lectores, la información que "ejecutan" en una aplicación digital, como una computadora, está en forma digital, es decir, son dos niveles de tensiones que representan el cero o nivel bajo (L0) y el "uno" o nivel alto (HI). Estos niveles se denominan "niveles lógicos" y un "cero" o un "uno" consiste en la unidad mínima de información o "bit".
Todas las informaciones que forma parte de un programa, y con la que funcionan las computadoras y otros equipos, consisten en agrupaciones de ceros y unos que se denominan "palabras" o "bytes". Ya lo hemos estudiado en los primeros capítulos de este curso.
Los primeros tipos de memorias que se utilizaron para almacenar estas informaciones, en forma de bytes, se formaron mediante anillos magnetizables, en la disposición que se muestra en la figura 132.
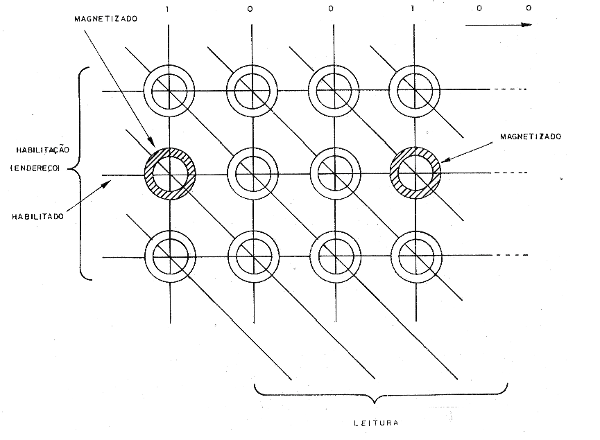
Así, los anillos pequeños del metal fueron atravesados por los alambres en los cuales los bits fueron aplicados, es decir, los niveles de tensión correspondiendo a los bits.
Para almacenar el byte 100100, por ejemplo, por un instante el primero y el cuarto alambres fueron atravesados por una corriente, mientras que los otros no.
En la carrera que serían los anillos que almacenarían esta información, el alambre horizontal fue atravesado por una corriente que "habilitó" el circuito. De esta manera, sólo los anillos atravesados por la corriente vertical de esa carrera se magnetizaron, registrando así la información.
En esa fila tuvimos el primer y cuarto anillo magnetizado, y los otros no, protegiendo así la "palabra" digital 100100.
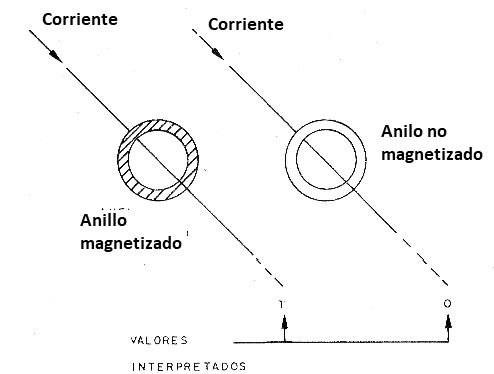
Para "leer" esta información, era suficiente volver a habilitar esta cola con una corriente adecuada y, aplicando los impulsos apropiados en la cola vertical, se obtuvo en la cola oblicua una señal de lectura. Para los alambres que pasan a través de un anillo no magnetizado tendríamos una corriente de salida, pero sería diferente en la salida de los anillos magnetizados, como se muestra en la figura 133.
En la figura 134 tenemos una foto de una antigua memo9ria de este tipo.

Evidentemente, este proceso además de ocupar un espacio razonable no era el más simple de operar, limitando la capacidad de los ordenadores antiguos.
La ventaja de esta memoria es que podría guardar la información incluso después de que el equipo se cerró. Por lo tanto, era una "memoria no volátil".
Un tipo de memoria que también se utilizó en los primeros ordenadores fue la que almacenó la información en circuitos. Su desventaja era que, cerrando la computadora, la información de estas memorias se perdió. Por lo tanto, era una memoria "volátil".
Para almacenar información sobre el circuito se utilizaron configuraciones que ya hemos estudiado en capítulos anteriores, los flip-flops.
Un antiguo flip-flop, utilizando válvulas como en los primeros ordenadores, se muestra en la figura 135. Ya hemos estudiado este circuito en capítulos anteriores de nuestro curso.
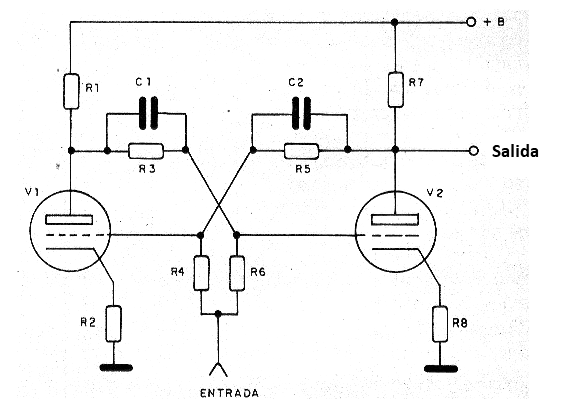
Veamos cómo funciona:
En los primeros tipos de flip-flops se utilizaron dos válvulas en la configuración indicada, pero luego con la aparición del transistor, se utilizaron dos transistores.
Este circuito funciona como una especie de "balancín" electrónico donde cuando un lado está en alto nivel el otro está en el nivel bajo. Esto significa que cuando un transistor (o válvula) está conduciendo (nivel bajo), el otro obligatoriamente es sin conducir o en el nivel alto. (vea más en los capítulos anteriores de este curso).
Para cada pulso de entrada el flip-flop "cambia el estado". De esta manera, la salida flip-flop puede estar en el nivel alto o en el bajo, dependiendo del comando que recibe, almacenando así un cero o un Uno (LO o HI). Cada flip-flop es por lo tanto una "memoria" de un bit.
Con el descubrimiento del circuito integrado, hemos tenido grandes avances en la fabricación de memorias, así que básicamente a día de hoy tenemos en nuestras computadoras estas dos modalidades de almacenamiento de información.
Si para almacenar un bit simple necesitamos una buena cantidad de componentes, lo que no dice la gran cantidad de información con la que funcionan los equipos. Y la mayoría de los equipos digitales modernos.
Un ordenador personal de tipo PC, por ejemplo, puede tener memorias capaces de trabajar con 500 megabytes (500 millones bytes), e incluso más cada byte con 8, 16, 32 y hasta 64 bits.
Esta enorme capacidad de almacenamiento sólo es posible con el uso de circuitos integrados.
El circuito completo de un flip-flop se puede fabricar en unos pocos milímetros de silicio. Más que eso: en un solo inserto de silicio o "chip" podemos montar miles e incluso millones de componentes formando miles o millones de flip-flops ya organizadas para almacenar información.
Incluso podemos fabricar otras configuraciones de componentes que sean capaces de almacenar información y algunas de forma permanente.
A continuación, tenemos en forma de circuitos integrados dos tipos de memorias: volátiles y no volátiles, con gran capacidad de almacenamiento y que se utilizan no sólo en ordenadores, sino en muchas otras aplicaciones.
Para que los datos que deben ser grabados se puedan colocar en una memoria y después leídos, deben tener una organización que incluya la existencia de pinos de acceso y también pinos de direccionamiento, es decir, pinos que puedan decir dónde se graban las informaciones.
A través de estos pinos de direccionamiento también podemos localizar la información deseada cuando necesita ser leída. En la figura 136 tenemos la organización típica de una memoria, con el uso de ambos términos en portugués, inglés y español.
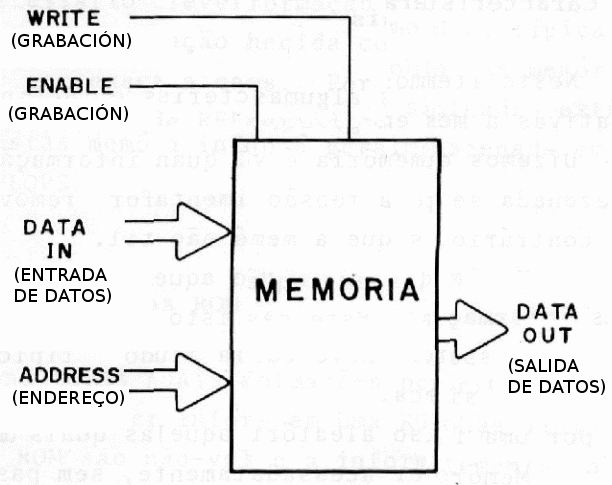
Una memoria se organiza de tal manera que contenga una cierta cantidad de líneas, y cada línea tiene tantas posiciones como los bits grabados. Por ejemplo, una memoria de 1024 líneas con 8 posiciones, puede grabar 1024 bits (1 KB) de 8 bits.
Para grabar la línea de grabación y activar y los datos se colocan, un byte a la vez, en la línea de entrada de datos. Si la memoria tuviera 8 bits por línea, esta línea tendrá 8 entradas.
La ubicación donde se deben grabar los datos se determina por los niveles de la entrada de dirección. Por ejemplo, para las direcciones 1024, necesitamos tener 10 líneas de dirección, para que puedan llegar a todas las posiciones, pues 210 – 1024.
En el momento en que se activa la entrada habilitación, los datos pasan a la memoria donde está grabado.
Para leer los datos, la entrada de grabación está deshabilitada y colocando la dirección de la posición donde se encuentra el dado en la entrada de DIRECCIÓN, el dato grabado aparece en la salida.
Vea que si conectamos la entrada de dirección en un circuito de conteo secuencial, la lectura de los datos es secuencial, y aparecerán en el orden en que fueron grabadas, en la salida de la memoria;
13.2- Tipos de Memorias
Existen varias tecnologías para almacenar información en chips, lo que lleva a muchos tipos de memorias, empleadas en una multitud de aplicaciones electrónicas.
Analicemos los principales tipos de memorias:
13.2.1 - ROM
Read-Only Memory, o Memorias de sólo lectura, son circuitos fabricados de tal manera que, en el propio proceso de fabricación, ya son grabadas las informaciones que deben contener.
Esto se logra a través de una máscara que determina cómo será el circuito integrado y que ya tiene en su diseño la configuración con la información que debe ser grabada.
El pequeño chip de silicio que contiene la información definitiva se coloca en una cubierta, como en la figura 137, es utilizada.

Las informaciones contenidas en esta memoria, como su nombre lo indica, sólo puede ser leída, y no alterada por ningún tipo de acción externa. En otras palabras, el fabricante determina la información que este tipo de memoria contendrá antes de fabricarla.
Se trata de una memoria no volátil, ya que la información grabada se retiene, incluso después de que el circuito en el que se encuentra está desconectado.
En la práctica estas memorias encuentran muchas aplicaciones como, por ejemplo, retener información importante para el uso de un aparato, incluso cuando se apaga, por lo que después de ser conectado funciona normalmente.
Por ejemplo, en un teléfono móvil ellas conservan la información sobre las configuraciones originales del fabricante, y en los computadores estas memorias contienen las informaciones necesarias para el proceso de arranque (boot) en el momento en que él es conectado.
13.2.2 - PROM
Programable Read-Only Memory o Memoria Programable Sólo de Lectura es una memoria no volátil, ya que incluso después de desconectar su alimentación, todavía mantiene los datos almacenados en el interior.
La diferencia, en relación con el tipo anterior, es el hecho de que pueden ser programados por el usuario.
En esta memoria se utilizan micro transistores o incluso líneas de semiconductores de silicio que funcionan como fusibles y que por lo tanto pueden ser "quemados" por una corriente especial.
En la práctica, estos fusibles se fusionan con una temperatura de 1000o C lo que se obtiene con una corriente del orden de 15 mA. Ésta es entonces la corriente de programación de este tipo de memoria.
De esta manera, cuando compramos un recuerdo de este tipo, todos los fusibles son cortos (buenos) y, con esto, la memoria sólo contiene ceros.
La grabación se realiza quemándose en la misma fila el micro fusibles en el que se desea grabar el nivel HI o 1, como se muestra en la figura 138.
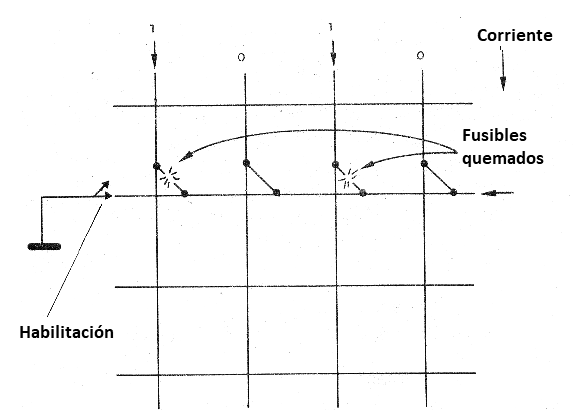
Con el paso de la intensa corriente los transistores-fusibles "abren" y en este punto tenemos un alto nivel o 1 grabado.
Vea, por lo tanto, que una vez hecho la grabación no es posible "Desgravar" esta memoria para hacer una corrección. Una vez que "quemado" el transistor no tiene ¡vuelta!
Es por eso que decimos que se trata de una memoria de sólo lectura si se puede grabar (programar) una vez: una vez grabada no es posible cambiar su contenido.
En la automatización, estas memorias se pueden utilizar para almacenar la rutina operativa de una máquina, determinando la secuencia de funciones que debe realizar.
13.2.3 – RAM
Random Access Memory o es una memoria que tanto puede ser grabada como leída en cualquier momento. El término "aleatorio" significa que podemos leer o grabar en cualquier momento una información que esté en cualquier lugar de esta memoria.
Este tipo de memoria es muy importante en el equipo digital, ya que se utiliza para guardar los datos que se usan y por lo tanto están cambiando cada instante de acuerdo con el programa "roda".
En los computadores ellas almacenan información que cambia constantemente durante la ejecución de un programa, la digitación de un texto, recibiendo datos de Internet o todavía el procesamiento de una imagen
Estas memorias son volátiles, porque cuando el ordenador, o cualquier otro equipo en el que está presente está desactivado, toda la información que contiene se pierde, lo que significa que si necesitamos tener esta información permanentemente, debemos antes transferirlas a otro tipo de memoria que no sea volátil.
Eso es lo que hacemos cuando transferimos el resultado de un trabajo en el ordenador al disco duro, a un CD o a una memoria USB (pen drive).
Estas memorias están formados básicamente por una gran cantidad de flip-flops del tipo CMOS que se montan en una pequeña plaquita de silicona, como se muestra en la figura 139.
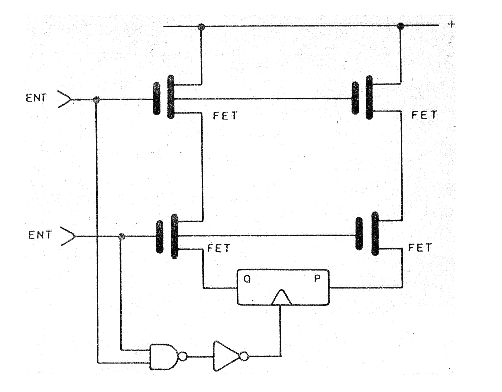
Cada flip-flop como vimos, almacena 1 bit, lo que significa que para almacenar 1 megabyte o 1 millón de bytes de 16 bits en una memoria de este tipo necesitamos ¡16 millones de flip-flops! La tecnología moderna logra "fabricar" esta enorme cantidad de flip-flops en unas placas de silicio pocos milímetros.
En esta pastilla es colocada una cubierta, como la de la figura 140, donde los pinos dan acceso a los flip-flops y otros circuitos de control interno.

Vea que no es necesario tener un pino para cada flip-flop. Lo que se hace es "arreglar" los flip-flops para que puedan ser activadas por medio de direcciones, como vimos al analizar la operación.
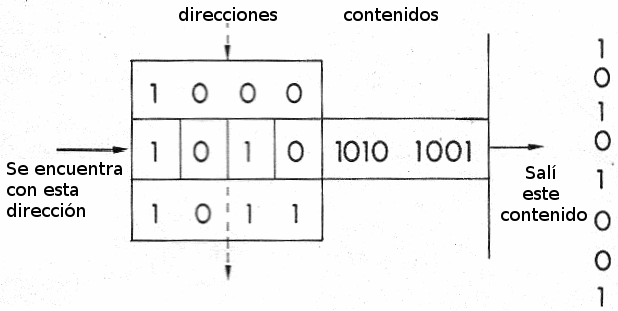
Por ejemplo, si queremos grabar o leer el contenido de un byte determinado, lo que hacemos es activar los pinos que dan su dirección con el código correspondiente, por ejemplo 1010 1001. Al mismo tiempo, informamos al pino de R/W (lectura o grabación) si estamos leyendo o grabando una información.
Con esto el circuito interno, pone en los pinos de salida lo que está contenido en la "dirección" solicitada, todo como se muestra en la figura 141.
13.2.4 – EPROM
El nombre de esta memoria proviene de la abreviatura de Erasable/Programable Read-Only Memory o Memoria Programable y Borrable Solamente de Lectura.
De una manera simple, se trata de un EPROM que puede ser borrado. Por esta razón, estas memorias son muy populares entre los proyectistas, ya que podemos reutilizarlos muchas veces, grabando y borrando las informaciones deseadas.
Esta memoria se fabrica de tal manera que una fuerte radiación ultravioleta puede modificar el estado de conducción de los elementos del chip que almacenan la información.
Típicamente, estos elementos contienen cargas eléctricas que se fijan más o menos definitivamente en ciertas regiones cuando se programa, así determinando si la salida de la célula será un "cero" o un "uno" según el bit almacenado.
Para que esta información se borre, el circuito integrado tiene una ventana de cuarzo que permite que la radiación ultravioleta pase, como se muestra en la figura 142.

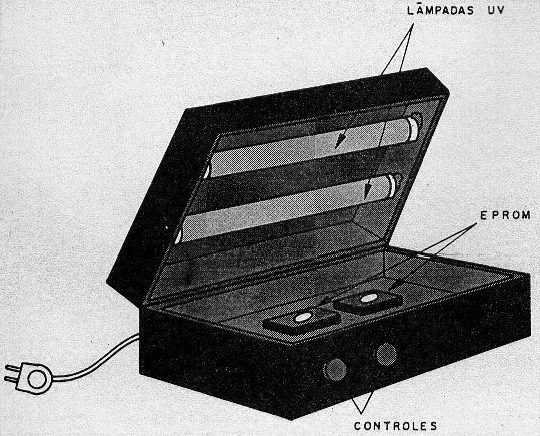
Para borrar la información grabada, exponemos los memorias a la radiación de una lámpara ULTRAVIOLETA especial (UV), que se realiza a través de un aparato apropiado, como se muestra en la figura 143.

En la figura 144 tenemos un borrador de EPROM de construcción casera. Tenga en cuenta que las lámparas utilizadas son de tipo especial, y nunca debe ser expuesto, ya que la radiación es muy peligrosa, especialmente si se centra en los ojos.
Una serie popular y EPROMs está formada por los tipos 2708, 2716 y 2732, 2764, 27128 y 27512 con diversas capacidades y organizaciones. Vamos a analizar las características de algunos de ellos de una manera introductoria, como para obtener información más completa, el lector debe consultar sus Datasheets.
2716
Dependiendo del fabricante y de la tecnología empleada podemos encontrar prefijos y letras intermedias que indiquen las características de los componentes. Los detalles, por supuesto, deben ser consultados en las Datasheets de cada uno, antes de ser utilizados.
El 2716, como su nombre indica, es una memoria de 16k donde tenemos 2k líneas de 8 bits. Es una memoria de 2k x 8, como se indica en los manuales o en los circuitos.
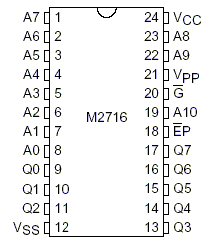
A continuación, hay 2048 posiciones de memoria a las que se puede acceder por 11 líneas de direcciones (address lines), como se muestra en el pinaje con la tabla de información en la figura 145.
|
Pin Number |
Description |
|
|
1 |
A7 - Address Input |
|
|
2 |
A6 - Address Input |
|
|
3 |
A5 - Address Input |
|
|
4 |
A4 - Address Input |
|
|
5 |
A3 - Address Input |
|
|
6 |
A2 - Address Input |
|
|
7 |
A1 - Address Input |
|
|
8 |
A0 - Address Input |
|
|
9 |
Q0 - Data Input |
|
|
10 |
Q1 - Data Input |
|
|
11 |
Q2 - Data Input |
|
|
12 |
Vss - Ground |
|
|
13 |
Q3 - Data Input |
|
|
14 |
Q4 - Data Input |
|
|
15 |
Q5 - Data Input |
|
|
16 |
Q6 - Data Input |
|
|
17 |
Q7 - Data Input |
|
|
18 |
EP - Enable Programming |
|
|
19 |
A10 - Address Input |
|
|
20 |
G - Output Enable |
|
|
21 |
Vpp - Program Supply |
|
|
22 |
A9 - Address Input |
|
|
23 |
A8 - Address Input |
|
|
24 |
Vcc - Positive Power Supply |
|
Esta memoria tiene salidas tri-state, debe ser alimentada por una tensión de 5 V. Las líneas A0 a A10 son las líneas de dirección, y las entradas G y EP deben colocarse en el nivel 0 para tener acceso a los datos de la salida.
Las entradas y salidas de esta memoria son compatibles con la tecnología TTL y se pueden encontrar en varias versiones con diferentes sufijos que indican el tiempo de acceso. Los tiempos de acceso que pueden variar entre 350 ns y 650 ns son parámetros importantes cuando se trabaja con una memoria.
Indican cuánto tiempo necesitamos para transferir información a la memoria y cuánto tiempo necesitamos para leer esta información, expresada en nanosegundos;
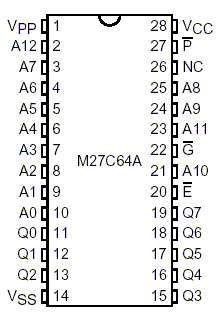
Otra memoria de esta familia es el 2764 que tiene 8 k líneas de 8 bits, según el pinaje y la tabla demostrados en la figura 146.
|
Pin Number |
Description |
|
1 |
Vpp - Program Supply |
|
2 |
A12 - Address Input |
|
3 |
A7 - Address Input |
|
4 |
A6 - Address Input |
|
5 |
A5 - Address Input |
|
6 |
A4 - Address Input |
|
7 |
A3 - Address Input |
|
8 |
A2 - Address Input |
|
9 |
A1 - Address Input |
|
10 |
A0 - Address Input |
|
11 |
Q0 - Data Input |
|
12 |
Q1 - Data Input |
|
13 |
Q2 - Data Input |
|
14 |
Vss - Ground |
|
15 |
Q3 - Data Input |
|
16 |
Q4 - Data Input |
|
17 |
Q5 - Data Input |
|
18 |
Q6 - Data Input |
|
19 |
Q7 - Data Input |
|
20 |
E - Chip Enable |
|
21 |
A10 - Address Input |
|
22 |
G - Output Enable |
|
23 |
A11 - Address Input |
|
24 |
A9 - Address Input |
|
25 |
A8 - Address Input |
|
26 |
NC - Not Connected |
|
27 |
P - Program |
|
28 |
Vcc - Positive Power Supply |
13.2.5 - EEPROM
Lo que tenemos es la abreviación de Electrically Erasable/Programable Read-Only Memory o Memoria de sólo lectura borrable y programable eléctricamente.
Estas memorias encuentran una cantidad cada vez mayor de usos en circuitos digitales, y en muchos casos se incluyen en otros chips, tales como microcontroladores y microprocesadores.
De esta manera, muchos dispositivos que utilizan chips con estas memorias no requieren memorias externas para grabar datos que deben permanecer incluso después de que se desconecten.
Para programar esta memoria simplemente utilice señales eléctricas del propio circuito, como en el caso de una RAM, y para borrar estas informaciones, simplemente aplique una señal eléctrica de ciertas características.
Además, es una memoria no volátil, es decir, una memoria que mantiene las informaciones incluso después de que su energía está apagada. En la figura 147 tenemos un ejemplo de EEPROM.

También debemos tener en cuenta que a medida que aumenta la capacidad de almacenamiento, el número de pinos también, lo que puede hacer el chip demasiado grande, que es un inconveniente para ciertas aplicaciones.
En la figura 148, tenemos un ejemplo de memoria de este tipo.

13.3 – Los Convertidores A/D
Equipos digitales, microcontroladores, controles industriales, computadoras y muchos circuitos que procesan los datos obtenidos de los sensores operan exclusivamente con señales digitales. Por lo tanto, si en la salida de un sensor tenemos una señal analógica y necesitamos transferir esta señal a un circuito digital, como un ordenador tendrá que "convertirlo".
Para convertir una señal de la forma analógica a la forma digital, usamos una configuración denominada convertidor analógico/digital, ADC o simplemente convertidor A/D. Estos convertidores son ampliamente utilizados en la adquisición de datos y control que Interactúan ordenadores con dispositivos de medida.
En los laboratorios, por ejemplo, se puede utilizar un convertidor de este tipo en un sistema de adquisición de datos para convertir las indicaciones de un sensor de temperatura en una forma digital que el ordenador puede procesar, y tomar decisiones para activar circuitos externos, o simplemente almacenar las temperaturas a horas programadas en la memoria, como se muestra en la figura 149.
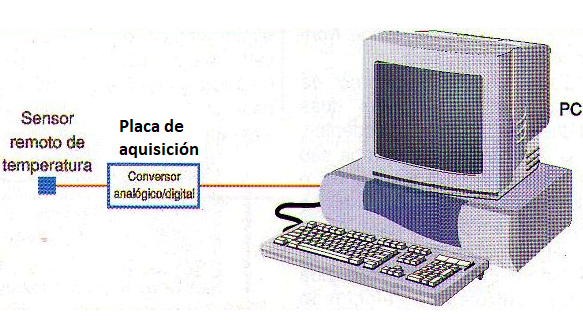
Para entender cómo funcionan los convertidores analógico/digital o analógico al digital, primero necesitamos entender las diferencias entre los dos tipos de cantidades.
Si usamos un sensor, como un NTC (Negative Temperature Coefficient Resistor ), para medir las temperaturas, tenemos una señal analógica en su salida, es decir, una tensión análoga a una determinada temperatura. En este sensor, como se muestra en el gráfico de la figura 150, tenemos una correspondencia directa entre la temperatura y la resistencia presentada.
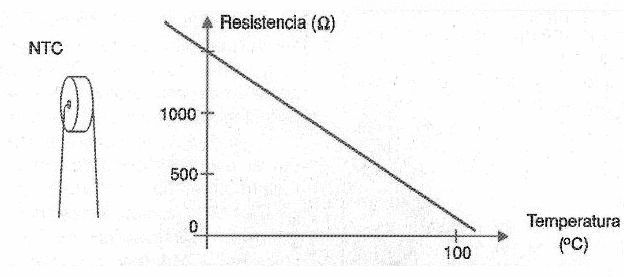
Esto significa que entre los dos extremos de temperatura en los que se puede utilizar este sensor, hay infinitos valores posibles. Decimos, en estas condiciones, que el rango de cobertura de este tipo de sensor es continuo y que hay una analogía entre la temperatura y la resistencia.
Por lo tanto, es un sensor que proporciona una salida analógica.
Podemos convertir esta salida de resistencia a otras cantidades que también pueden variar continuamente, como la presión, el nivel de un depósito, etc., en otras cantidades eléctricas que también pueden variar en bandas continuas como la tensión y la corriente.
Podemos hacer perfectamente que la tensión varíe continuamente entre dos valores, entre los cuales este sensor debe funcionar, como se muestra en la figura 151.
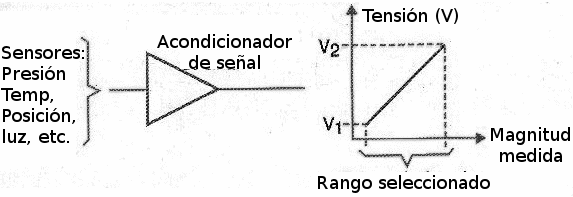
Por supuesto, las cosas no siempre son tan simples: Supongamos que en lugar de convertir la temperatura en resistencia, queremos hacer su indicación por una escala de LEDs, como se muestra en la figura 152.
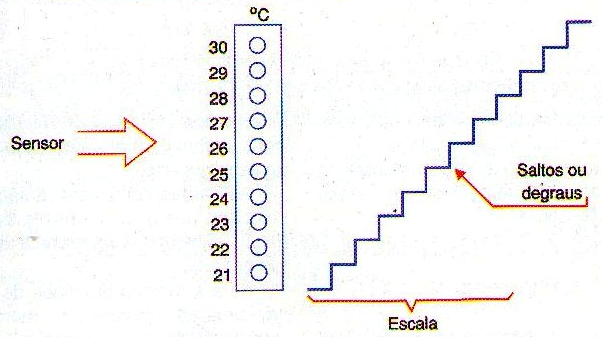
Si cada LED indica un grado, y tenemos 10 LEDs para medir temperaturas de 20 a 30 grados centígrado, es evidente que no podemos tener una indicación de valores de temperatura que no están representados por números enteros. El sistema no puede indicar 22,4 o 22,6 grados centígrados. O indica 22 o 23.
Si queremos tener mayor precisión en la indicación con este tipo de indicador, necesitamos más LEDs. Con 20 LEDs podemos tener la indicación intermedia en medio grado en la escala indicada. Sin embargo, lo que está claro es que, con este sistema, las indicaciones sólo pueden ocurrir "en saltos" y que estos saltos tienen valores bien definidos.
Decimos que en este caso, la indicación se produce de manera discreta y los LEDs pueden asociarse con cantidades o dígitos bien definidos. Por lo tanto, si vamos a utilizar una representación digital en forma binaria, podemos asociar los 10 estados indicativos de los LEDs con una escala de 10 LEDs.
Como tenemos 10 estados posibles para los LEDs, cuatro bits son suficientes para representarlos a todos. Sin embargo, si necesitamos una definición más alta para las indicaciones, por ejemplo, con 20 LEDs y media indicación en medio grado necesitamos al menos 5 bits.
En la práctica, las indicaciones que cubren una escala con unos pocos puntos no son interesantes, ya que no significan una buena exactitud. Cuantos más puntos tenga la "escalera" de las indicaciones, mejor será la precisión en la conversión de la magnitud, por ejemplo, la resistencia de un sensor.
Un convertidor A/D que tiene una salida de 4 bits tiene 16 "escalones" de indicación, o puede establecer una escala de 16 valores diferentes. Ya, un indicador de salida de 8 bits, puede establecer una escala con 256 valores diferentes, 1 de 12 bits puede establecer una escala de 4096 puntos y un de 16 bits puede establecer una escala de 65 536 puntos, como se muestra en la figura 153.
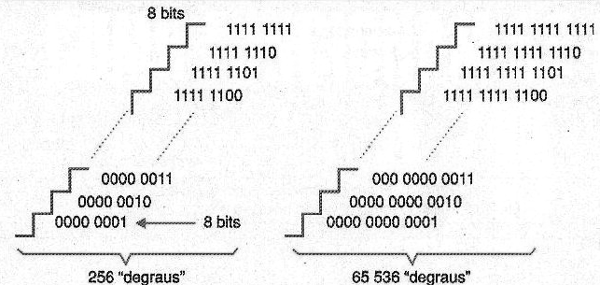
Vea entonces que para un convertidor A/D que puede fijar 256 valores diferentes en una escala de medidas tiene una mejor exactitud que 0,4% y con 4096 diferentes valores en una escala de medidas tenemos una mejor exactitud que 0,024%.
Los convertidores A/D existentes en el mercado tienen precisamente estas características.
13.3.1 – Los Convertidores en Práctica
Por supuesto, la escala de LEDs no corresponde a lo que deseamos en la práctica para un convertidor. Para 10 LEDs disponemos de una salida para cada LED que hará su activamente directo. Sin embargo, no podemos tener 4096 salidas en un convertidor que funciona en una escala de 16 bits.
Es mejor tener acceso directo a los bits y con esto equipar el circuito de 16 salidas. En la figura 154 tenemos un ejemplo de cómo se puede hacer esto.
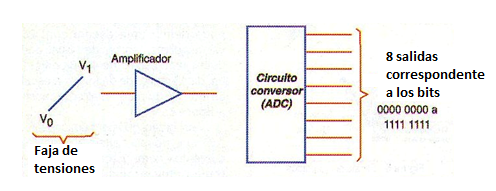
El circuito entonces cuenta con una entrada en la que aplicamos la señal analógica, siendo normalmente especificado un rango de tensiones para la conversión. Por ejemplo, si el circuito convierte las señales en el rango de 0 a 1 Volt, debemos tener cuidado de que el sensor utilizado (o la fuente de información analógica) funcione en esta pista.
Un amplificador operacional puede tener su ganancia programada para hacer justamente eso. Las salidas consisten entonces en 16 pinos en los que se obtienen los niveles lógicos 0 o 1 según la tensión de entrada.
Para la mayoría de los tipos de convertidores A/D del mercado, estas salidas son compatibles con la tecnología TTL (nivel alto con 5V y nivel bajo con 0V) se puede conectar directamente al puerto de I/O de un ordenador, como se muestra en la figura 155, o incluso CMOS donde los 5 V de alto nivel también se puede utilizar sin problemas.
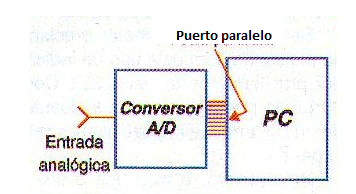
A continuación, programe el ordenador para "leer" los valores del puerto en el instante deseado, y hacer la conversión a la escala deseada. Por ejemplo, si el rango de entrada que corresponde a temperaturas de 0 a 30 grados centígrado y, que a su vez conducen a tensiones a la entrada del convertidor de 0 a 1 Volt, el convertidor generará en sus valores digitales de salida entre 0 y 4096 (si es 12 bits).
El ordenador debe programarse para dividir la escala de 0 a 30 grados centígrados en 4096 valores (cada unidad de lectura corresponderá a 0,00732 grados).
El valor 010010010010 (binario) leído en la entrada IO o salida del convertidor que corresponde a 1070 (decimal), es equivalente a una temperatura de 8,5644 grados centígrados.
13.3.2 - Cuantización
Los valores instantáneos de la tensión de la señal de entrada, que se obtienen en la salida del circuito de muestreo y retención. Necesidad de convertirse en formato digital. Este proceso se da el nombre "Cuantización".
Los DSPs (Procesadores de Señales Digitales – que estudiaremos en el capítulo siguiente) procesan las señales analógicas convertidas al formato digital utilizando este proceso. Lo que un DSP puede hacer con la señal dependerá precisamente de la exactitud con la que se realiza la cuantización.
La representación de los valores instantáneos que se muestran por los circuitos anteriores depende del nivel de cuantización realizado, es decir, cuántos bits se utilizan para representar cada valor que se muestra.
Así que, como hemos visto, si usamos 2 bits tendremos una precisión menor que si usamos 4 bits para hacer la cuantización, como se muestra en la figura 156.
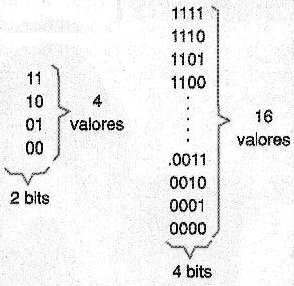
Comparando, en cada caso, los niveles cuantizados en los dos ejemplos, podemos percibir fácilmente los errores introducidos en el proceso, como se muestra en la figura 157.

En los ejemplos que dimos, los niveles de cuantización eran muy bajos, entonces aparecieron grandes errores. En la práctica, los DSPs utilizan niveles de cuantización de 10 o 12 bits e incluso más, lo que resulta en un error insignificante.
Le recordamos que esta es una de las desventajas de operar con señales en la forma digital, porque su representación sólo se puede hacer en "escalones" cuya altura determinará el grado de exactitud. Cuanto mayor sea el número de escalones que se pueden utilizar, mayor será la precisión en el valor analógico que se representa
13.3.3 – Los circuitos de los Convertidores A/D o ADC
Para realizar una conversión A/D como en la escala de LEDs podemos tener circuitos relativamente sencillos. Se puede utilizar una escala simple de comparadores que tienen diferentes tensiones de referencia como se muestra en la figura 158.
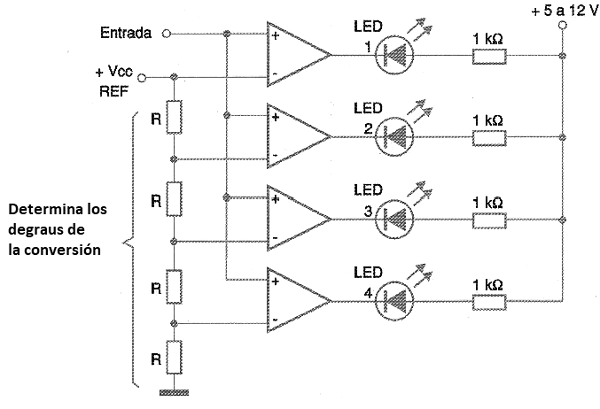
Cada vez que la tensión de entrada alcanza el nivel de disparo de uno de los comparadores del conjunto, cambia, conmuta el LED correspondiente o cambia el nivel lógico de su salida.
Este tipo es secuencial con un comportamiento que no es muy interesante en las aplicaciones más críticas: cada vez que un comparador cambia porque se alcanza su nivel de unidad, el anterior que se cambió no vuelve al estado inicial.
Con un circuito más sofisticado podemos obtener esta conmutación y así pasar de un sistema de barra móvil a un punto movible, como se muestra en la figura 159.
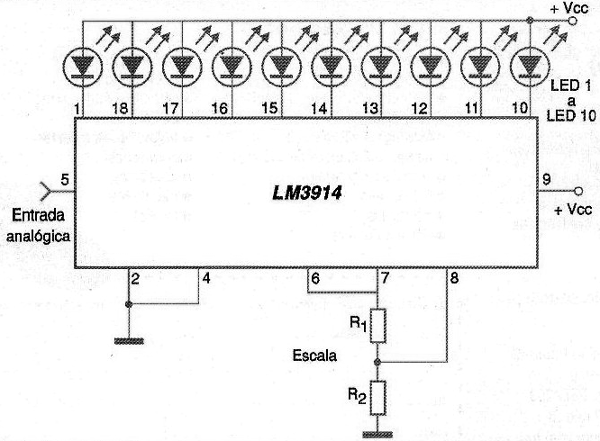
Pero para las aplicaciones que implican la adquisición de datos, este tipo de convertidor no cumple con las necesidades más críticas: necesitamos convertir los niveles en indicaciones en decimal codificado en binario, binario puro, o incluso hexadecimal, para obtener la mayor definición posible y compatibilizar el circuito con la tecnología digital más común.
Esto se puede hacer con la ayuda de circuitos más complejos, que además de los comparadores implican configuraciones lógicas y también otros circuitos que facilitan su uso.
Para entender mejor cómo funcionan estos circuitos debemos comenzar como la forma en que se debe hacer la muestra de la señal que es un bloque común a todos los convertidores que es el circuito de muestra y retención (sample and hold):
13.3.4 - El circuito de captura (o mustreo) y retención o "sample and hold":
El valor de las señales analógicas que se deben convertir a la forma digital, corresponde a un cierto instante cuya duración, en algunos casos no va más allá de unas pocas millonésimas de segundo.
Por lo tanto, un primer bloque importante del convertidor es un circuito que lee el valor de la señal que se convertirá en un cierto instante, y lo almacena.
Con esto, incluso si la señal oscila después, los circuitos que hacen la conversión tienen una memoria de su valor. Este circuito se muestra en bloques en la figura 160.
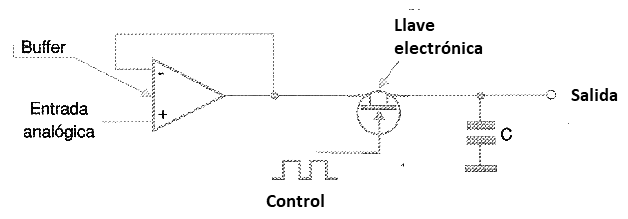
La señal a ser mostrada es amplificada por un buffer de entrada, cuyo propósito no es cargar el circuito externo y, al mismo tiempo, proporcionar aislamiento del circuito de conversión.
A la salida de este circuito tenemos una llave electrónica, o conmutador, que determina el momento exacto en el que se debe realizar la lectura de la señal. La llave se cierra por una fracción de segundo (en una frecuencia que depende de la velocidad de muestreo), permitiendo que la señal cargue el capacitor C.
Por lo tanto, cuando se abre la llave, esperando la siguiente lectura, el capacitor ha almacenado el valor de la magnitud analógica que se convertirá. Esta tensión en el capacitor se mantiene en el circuito del convertidor a través de un búfer de salida, durante el tiempo que necesite hacerlo.
En la figura 161 mostramos un gráfico donde representamos cómo oscila la tensión de entrada, y el circuito de muestreo y retención mantiene la salida constante durante los intervalos de conversión (que corresponden a los "escalones").
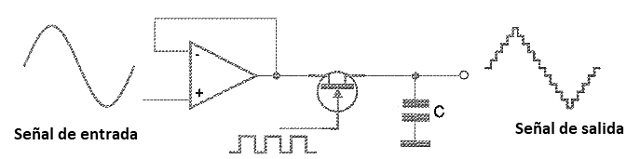
Para hacer el muestreo y la retención de una señal, entonces tenemos su conversión a forma digital hay varios sistemas. Estudiaremos a partir de ahora los principales sistemas.
13.3.5 – Sistemas de conversión
a) Sistema de conversión simultánea
El sistema de conversión simultánea (que es el más simple) tiene la configuración mostrada en la figura 162.
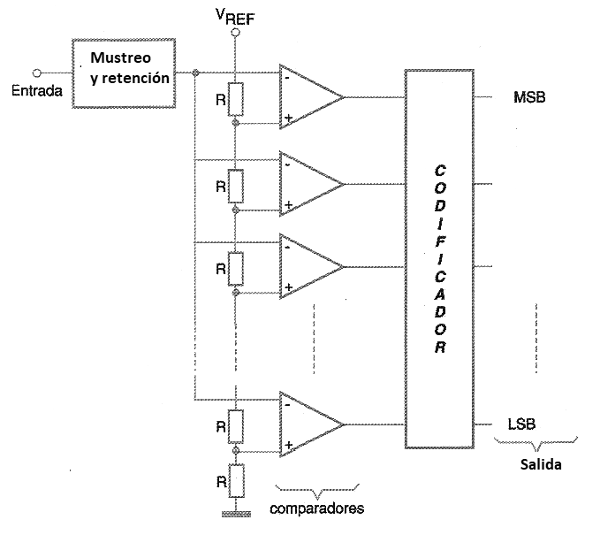
En este circuito, tenemos una escala de 8 valores de salidas posibles, que pueden ser cubiertos por un sistema de 3 bits. Por lo tanto, es un convertidor A/D de 3 bits.
Los comparadores tienen en sus entradas de referencia tensiones escalonadas que determinan el instante en que deben conmutar. Así pues, para 8 niveles para activar, tenemos 7 tensiones escalonadas a partir de 1/8 a 8/8 Vcc, que es la máxima tensión que el circuito puede medir en su entrada.
Evidentemente, este tipo de circuito está severamente limitado por el número de comparadores que podemos utilizar. Para un sistema de 16 bits, por ejemplo, ¡4095 comparadores serían necesarios!
Volviendo al circuito, los niveles lógicos obtenidos en las salidas de los comparadores son secuenciales, como hemos visto. Para obtener una salida codificada binaria, necesitamos usar una matriz de codificación.
Esta matriz se puede elaborar en esta configuración más simple de los inversores, puertos AND y puertos OR. De esta manera obtenemos señales que corresponden a los 8 niveles de tensiones posibles, a saber:
En este circuito tenemos un sistema adicional de RESET y puerto de lectura (READ). El puerto de lectura es interesante, ya que permite transferir los datos digitales al circuito externo sólo en el momento que deseamos. Así que podemos darle tiempo al circuito para estabilizarse.
Al aplicar esta entrada (READ) un pulso de corta duración, leemos el valor escaneado en ese instante. En el circuito indicado, este valor se almacena en un registro formado por un conjunto de flip-flops.
Por lo tanto, este valor se fija en la entrada y puede seguir activado, por ejemplo, un indicador. Para la siguiente lectura, el valor almacenado en el registrador debe borrarse antes de realizar una nueva lectura. Esto se logra por medio de un pulso de RESET.
b) Circuito de Conversión de Contador
En la figura 163 tenemos un diagrama de bloques de un convertidor que utiliza esta técnica.
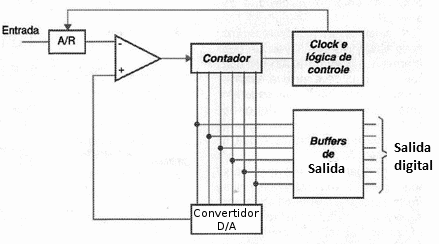
El comparador único con dos entradas se resalta en este circuito. Se aplica una entrada a la señal que se medirá (una tensión dentro de un rango de valores determinado). En la otra entrada aplicamos una señal que es producida por un generador especial llamado "generador de escalera".
Esta señal consiste en una tensión que se eleva "en saltos", con tantos escalones como sea necesario para la salida digital. Por ejemplo, en un convertidor de 8 bits, esta señal consiste en 256 "escalones" iguales a la tensión.
Una señal de este tipo puede ser generada fácilmente por un oscilador de clock que aplica su señal a un contador conectado a una red R/2R, como se muestra en la figura 164.
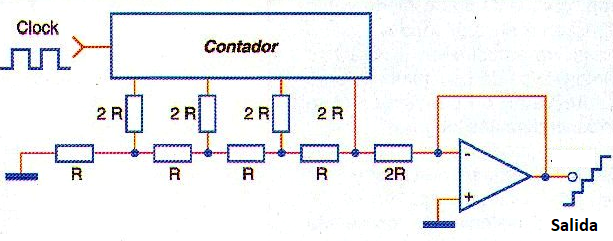
Observamos que el clock de este circuito está habilitado por el propio circuito comparador. Por lo tanto, suponiendo que hay una cierta tensión en la entrada.
Y la conversión se habilita, el oscilador de clock entra inmediatamente en operación. Suponiendo que el contador está en cero, entonces la producción de la "escalera" de la tensión comienza a aplicarse al comparador.
En el momento exacto la escalera genera un escalón que iguala la tensión de entrada, el comparador conmuta. El resultado de esto es la parada del clock y, por lo tanto. del recuento. En este momento el contador habrá registrado el número de escalones contados, es decir, sabrá en qué valor binario ocurrió la conmutación.
A continuación, transfiera este valor al circuito externo, lo que se puede realizar de la misma manera que en el proceso anterior a través de un registrador. Para la nueva conversión, que se puede hacer en una fracción de segundo más tarde, o mientras sea necesario, simplemente resetear el contador y rehabilitar el clock.
c) Convertidor para aproximaciones sucesivas
En la figura 166 tenemos un diagrama de bloques que representa este tipo de convertidor y donde analizaremos su operación.
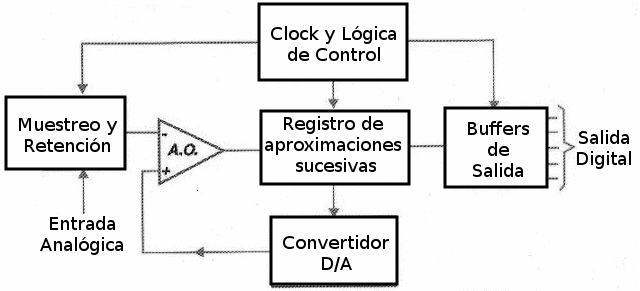
Como podemos observar, lo que distingue este circuito de lo anterior es el intercambio del contador por un registro de aproximaciones sucesivas, lo que lo hace mucho más rápido, no sólo reduciendo los tiempos de conversión, sino estandarizándolos, es decir, haciéndolos iguales Independientemente del punto de la escala en la que se encuentra la señal de entrada.
La señal aplicada a la entrada es retenida por el circuito de muestreo y retención, conectado a la entrada del comparador y, al mismo tiempo, activa el circuito de clock del sector de conversión digital.
Al iniciar la conversión, el registro de aproximaciones sucesivas comienza colocando a 1 bit más significativo (MSB) de la salida, aplicando esta señal al convertidor D/A. Si, con este procedimiento, la tensión aplicada por el convertidor D/A la entrada de referencia del comparador es mayor que la entrada, esto será un signo de que el valor que este bit representa es mayor que lo que desea convertir.
El comparador notifica esto al registro de aproximaciones, que luego devuelve el MSB a cero y coloca el bit que lo sigue inmediatamente a 1. Se hace una nueva comparación. Si el valor de tensión es ahora menor que la entrada, El bit se retiene probando lo siguiente colocando el 1. Si el valor se supera de nuevo, el comparador informa al registro y el bit vuelve a cero, pasando lo siguiente a 1 que se ha probado.
Cuando se prueban todos los bits, tendremos un valor binario muy cercano al deseado, dependiendo de la resolución del circuito. Probando todos los bits de esta manera, la conversión se convierte en muy rápido, ya que no tiene que esperar a que el recuento hasta el final, como se muestra en el gráfico en la figura 167.
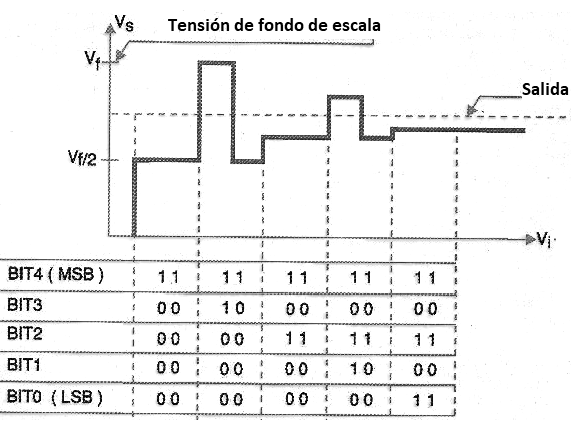
Vea que, mientras que en un convertidor de 8 bits por el método de rampa de escala que necesita para esperar a la cuenta hasta 256, en este convertidor debe esperar sólo 8 pruebas y comparaciones que se hacen. Por lo tanto, el circuito equivalente es 32 veces más rápido.
d)Convertidores de Rampa Simple
Este tipo de convertidor encaja en una nueva categoría formada por aquellos que utilizan integradores, siendo más sencillos que los anteriores, ya que no necesitan convertidores D/A. Los voltímetros digitales utilizan principalmente circuitos de este tipo.
En la figura 168 tenemos un diagrama de bloques que corresponde a un convertidor de este tipo, y que sirve como referencia para nuestro análisis operativo.
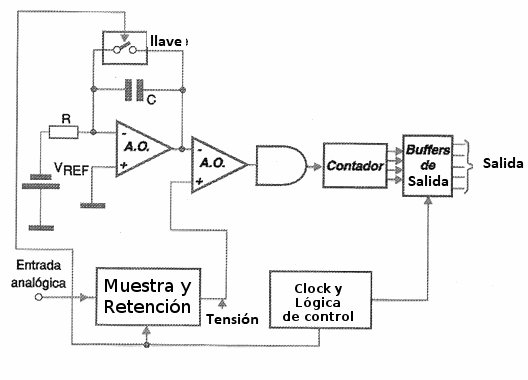
La señal analógica retenida del circuito de muestreo y retención también controla un Interruptor que activa un integrador. La tensión del integrador y la tensión mostrada se aplican al mismo tiempo en el comparador.
En el momento en que todo esto ocurre, un contador entra en funcionamiento, produciendo una salida digital progresiva.
El integrador está conectado a una fuente de tensión de referencia de tal manera que la tensión en su salida suba linealmente hasta que sea igual a la tensión mostrada. El momento en que esto ocurra detiene el recuento.
La velocidad del aumento de tensión en la salida del integrador determina la tasa de conversión, junto con el recuento. En el rango de funcionamiento del integrador, este tensión se eleva linealmente, y la frecuencia del clock contada por el contador corresponde digitalmente a los valores de la magnitud que se convertirá.
Por ejemplo, si tenemos un contador de 8 bits (hasta 256), se asegura de que el tensión del integrador se eleva, de un extremo a otro de la escala de tensiones de entrada analógica, en un momento que corresponde a 256 ciclos de clock.
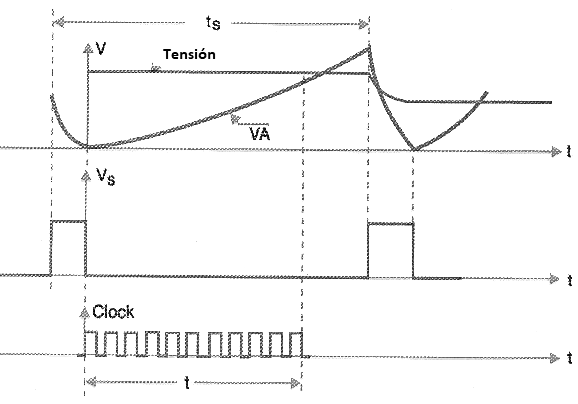
Cuando el recuento está paralizado, cuando se obtiene el valor digital, se puede aplicar a la salida del circuito. En la figura 169 tenemos las formas de onda de este circuito.
e) Convertidores de Doble Rampa
Un tipo que funciona mejor que el anterior es el convertidor de doble rampa, cuyo diagrama de bloques se muestra en la figura 170.
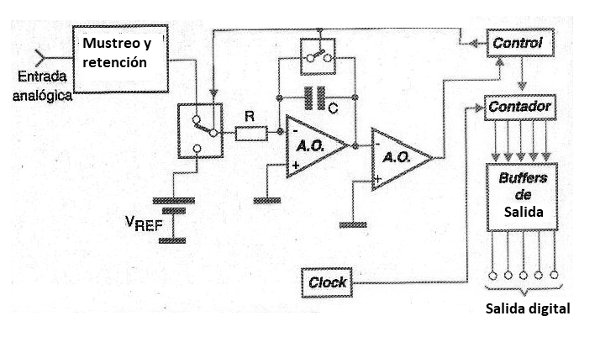
En este circuito, la señal muestreada y la señal de una fuente de referencia son clavadas por el clock de control y luego aplicadas a la entrada de un circuito integrador.
La rampa generada por la señal de entrada es negativa, mientras que la rampa generada por la señal de referencia es positiva. Dado que los dos están clavadas, la rampa final tiene una pendiente que depende de ambos. Como uno se fija, y el otro corresponde a la señal de entrada, usted puede utilizar la señal de salida a la llave el contador. Desde el contador, la operación es como en el tipo anterior.
f) Sigma-Delta
Este tipo de convertidor fue creado en 1962, pero sólo se utiliza en una escala más grande con el progreso logrado con las tecnologías VLSI.
La principal ventaja de este tipo de convertidor es su funcionamiento, en la mayor parte del circuito, hecho de forma digital. Es precisamente por estas características, además de otras ventajas, lo que hace posible integrarse fácilmente en la misma tableta de DSPs.
Otra ventaja que debe destacarse en este tipo de convertidor es que funciona con un ADC con sólo cuantización de 1 bit, operando a una frecuencia más alta que el límite Nyquist, seguido de un decimal en el dominio digital que disminuye la frecuencia de salida, aumentando así la exactitud.
Debido a que este tipo de convertidor es más importante para aplicaciones que involucran DSPs, un componente de vital importancia en la electrónica moderna, dedicaremos un poco más de espacio para explicar su principio de funcionamiento. Los ADCs de tipo Sigma-Delta operan basándose en un método que se emplea principalmente en la modulación de la señal de amplitud denominada "modulación delta".
En él, lo que se hace, no es convertir los valores absolutos muestreados, sino más bien las variaciones de valores entre los muestreos sucesivos. En la figura 171 representamos esto de una manera sencilla.
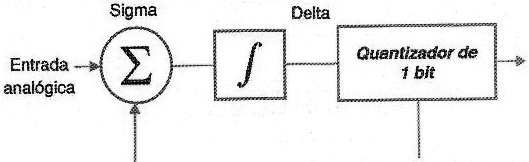
Un integrador se utiliza para este propósito, y como este tipo de circuito es lineal, su implementación es simple. Vea entonces que para una señal sinusoidal muestreada en (a), sólo tenemos la cuantización de las variaciones, lo que nos lleva a la representación de un bit sólo en (b) y también permite llegar a la reproducción de la señal en (c). El nombre Sigma-Delta proviene del signo de suma (Sigma) seguido del modulador Delta.
Para llegar al ADC Sigma-Delta completo, agregamos un ADC y un DAC de 1 bit y un filtro de decimación, como se muestra en el diagrama de bloques de la figura 172.
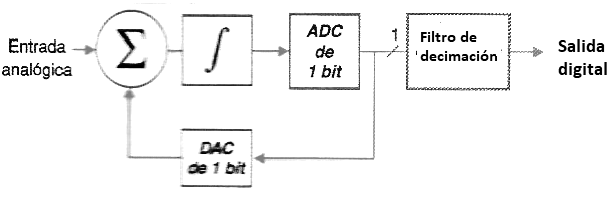
El propósito del filtro de decimación es disminuir la frecuencia con que los valores digitales son producidos.
Un punto muy importante a considerar en este tipo de filtro es que pueden ser implementados por los propios DSPs.
En la práctica, encontramos muchos circuitos integrados que hacen las operaciones que indicamos y que tienen las más diversas características.
Por lo tanto, en la búsqueda de un convertidor A/D para una aplicación determinada, debemos analizar las siguientes especificaciones:
a) Número de salidas o bits
Como ya hemos visto, este número es importante porque determina la resolución en la conversión A/D. Los valores entre 4 y 24 bits son comunes en el mercado, incluso en casos especiales en los que se pueden obtener más salidas.
Con la disponibilidad de microprocesadores de 32 bits y 64 bits, es posible confiar en convertidores compatibles.
Como ya hemos visto, un convertidor de 8 bits puede ser suficiente para aplicaciones industriales comunes e incluso menos críticas, confiando en 256 puntos de escala y 12 bits para 4096. Los 8 bits son especialmente interesantes para "casarse" con las características de los puertos paralelos de los ordenadores comunes (PCs).
b) Número de entradas
Los ejemplos que dimos, eran de convertidores sencillos en los que aplicamos en la entrada una sola señal. Sin embargo, hay convertidores A/D en forma de circuitos integrados que tienen varias entradas. Los tipos 2, 4 y 8 entradas son los más comunes.
Estos tipos hacen la lectura secuencial de las tensiones en sus entradas, convirtiendo los valores encontrados a la forma digital y, reproduciéndolos secuencialmente en las salidas. Eventualmente, usted puede seleccionar digitalmente por las entradas apropiadas que los sensores (o las entradas de datos) serán leídos lanzando los valores en la salida, tal y como se muestra en de la figura 173.
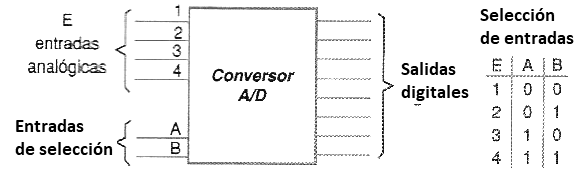
c) Velocidad
En la práctica, podemos encontrar aplicaciones donde la velocidad de conversión es muy importante. Si deseamos procesar una señal que oscila rápidamente Intensidad como, por ejemplo, una forma de onda de alta frecuencia y queremos diseñarlo en una pantalla de ordenador para usarlo como un osciloscopio.
Otra aplicación es convertir una señal de audio a la forma digital, para hacer su transmisión a un circuito de procesamiento remoto, en cuyo caso es necesario tener una velocidad de respuesta muy grande del convertidor.
Debe ser capaz de obtener al menos 2 muestreos por ciclo de señal que debe ser visualizado, es decir, debe tener una frecuencia de muestreo al menos 2 veces mayor que la frecuencia más alta de la señal de entrada.
Los convertidores con muchos mega Hertz de frecuencia de muestreo están disponibles para estas aplicaciones.
d) Rango de funcionamiento
El rango de funcionamiento no es realmente muy importante, ya que puede ser adecuado para circuitos externos conectados a la fuente de señal. Sin embargo, es necesario conocer esta pista, para que los circuitos puedan ser diseñados.
e) Compatibilidad lógica
Si vamos a utilizar el convertidor con microcontroladores, computadoras u otros dispositivos, necesitamos saber si es compatible con esta aplicación. La mayoría de los convertidores A/D tienen características de entrada y salida que permiten su conexión directa a ordenadores, microprocesadores y microcontroladores.
f) Linealidad
La curva de conversión de la grandeza analógica a la forma digital debe ser lineal a un buen convertidor. Esto significa que no hay desviaciones en la correspondencia entre el valor analógico y la salida digital a lo largo de la escala de valores en el que el convertidor debe funcionar. Sin embargo, en la práctica pueden producirse pequeñas desviaciones, como se muestra en la figura 174.
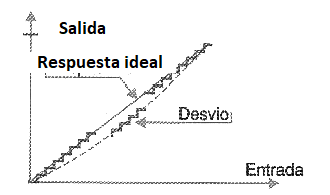
Esto significa que, en ciertos rangos de valores, la conversión puede ser menos precisa. Esta inexactitud es más severa en los tipos de definición más alta, porque las desviaciones pueden tener el mismo orden de magnitud que los "escalones" de la escala de conversión, afectando así a la precisión final de la conversión.
13.4 – Los DACs
Un DAC o Convertidor Analógico al Digital, convierte las señales digitales a una forma analógica, siendo así la inversa del ADC.
Los DACs suelen estar formados por una red R-2R, como se muestra en el circuito básico de la figura 175.
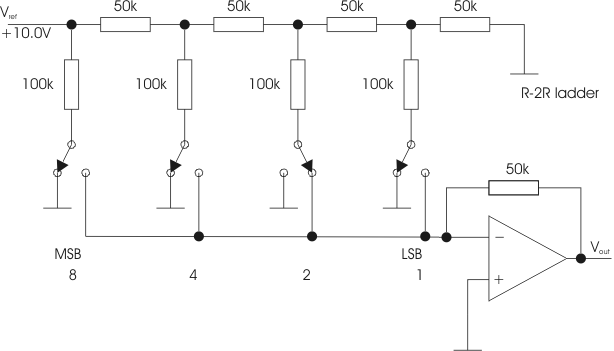
En lugar de las llaves mecánicas, como se indica en este circuito, se pueden utilizar los niveles digitales de un circuito.
Sumário
Curso de Electrónica - Electrónica Digital (CUR5000)
Curso de Electrónica - Electrónica Digital – Parte 1 (CUR5001S)
Curso de Electrónica Digital – Parte 2 - El Álgebra de Boole (CUR5002S)
Curso de Electrónica - Electrónica Digital - Parte 6 - Los Elementos Biestables (CUR5006S)
Curso de Electrónica - Electrónica Digital - Parte 9 - Contadores Digitales (CUR6002S)
Curso de Electrónica - Electrónica Digital - Parte 13 - Memorias, ADCs y DACs (CUR6006S)




