2.1 - El Álgebra de Boole
A mediados del siglo XIX George Boole, un matemático inglés, desarrolló una teoría totalmente diferente para el tiempo. Se basó en una serie de postulados y operaciones sencillas para resolver multitud de problemas.
Sin embargo, aunque el Álgebra Boole, como se llamaba, puede resolver problemas prácticos de control, fabricación de productos, instrumentación, etc., en el momento en que no había electrónica y ni siquiera las máquinas eran lo suficientemente avanzados como para utilizar sus principios.
El Álgebra de Boole llegó a ser importante con la llegada de la Electrónica, específicamente la electrónica digital que generó las computadoras modernas, los equipos digitales y las telecomunicaciones con las que estamos familiarizados.
Boole establece en su teoría que sólo hay en el universo dos condiciones posibles o estados, para el análisis de cualquier situación, y estos dos estados son opuestos.
Así, una lámpara sólo puede ser encendida o apagada; un grifo sólo puede abrirse o cerrarse; una fuente sólo puede tener o no tener tensión en su salida; una pregunta sólo puede tener una respuesta verdadera o falsa (sí o no).
Decimos de una manera sencilla que, en el Álgebra Boole, las variables lógicas sólo pueden adquirir dos estados:
0 o 1
Verdadero o falso
Abierto o cerrado
Alto o bajo (HI o LO)
Encendido o apagado
En electrónica digital, partimos precisamente del hecho de que un circuito sólo puede funcionar con dos estados posibles, es decir, podemos encontrar en este circuito dos tipos de señales: presencia de la señal o ausencia de la señal que lo hace perfectamente adecuado para los principios de la Álgebra de Boole.
Todo que un circuito de la lógica digital puede hacer es predicho por Álgebra de Boole. Desde las operaciones o decisiones más sencillas, como la iluminación de un LED cuando se activan dos sensores de cierta manera, o cuando se presiona una tecla, se gira en el espacio una imagen tridimensional.
A partir de principios simples, con reglas muy definidas, Boole demostró que desde operaciones sencillas como sumar y restar incluso las más complejas, que implican los cálculos realizados por ordenadores, pueden realizarse basándose en el concepto de sí o no o ausencia o presencia de una señal.
2.2 – Los niveles lógicos
Partimos entonces del hecho de que en los circuitos de lógica digital sólo podemos encontrar dos condiciones posibles: presencia y ausencia de señal. Lo hacemos para definir algunos puntos importantes para nuestro entendimiento.
En los circuitos digitales, la presencia de un tensión se indicará como en un 1 o HI (de HIGH o Alto), mientras que la ausencia de una tensión será indicada por 0 o LO (LOW o bajo).
El 0 o LO será siempre un tensión cero, o ausencia de señal en un punto de circuito, pero el nivel lógico 1 o HI puede variar según el circuito considerado, como se muestra en la figura 22.
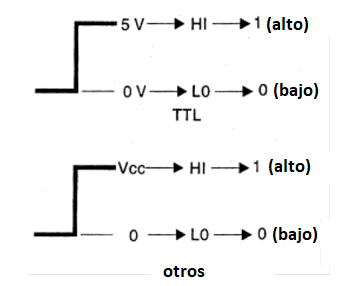
En la mayoría de los equipos digitales, llamados TTL, la tensión utilizada en la alimentación de todos los circuitos lógicos es de 5 volts, por lo que el nivel 1 o HI de sus circuitos siempre serán una tensión de 5 volts.
En el núcleo de algunos procesadores y en otras aplicaciones con batería, se puede encontrar una tensión de alimentación más baja, desde el orden de 3,3 volts y aún menos, lo que significa que en estos circuitos un nivel 1 o HI siempre corresponderá a una tensión de ese valor.
Hay también circuitos digitales que emplean componentes de la tecnología del CMOS y que se pueden accionar por tensión entre 3 y 15 volts típicamente. En estos casos, como se muestra en la figura 23, un nivel lógico 1 o HI puede tener cualquier tensión entre 3 y 15 volts, dependiendo sólo de la alimentación utilizada.
En la actualidad existen componentes de la tecnología LVT (Low Voltage Technology) o de muy baja tensión que pueden operar con tensiones muy bajas, en el rango de 0,8 a 1,2 V.
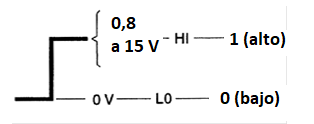
De hecho, la idea de asociarse la presencia de tensión en el nivel 1 la ausencia en el nivel 0 es una mera cuestión de convenio. Nada nos impide adoptar un criterio inverso y proyectar los circuitos sin que esto impida su funcionamiento normal.
Y esto realmente existe:
Así, cuando decimos que a alto nivel (1) asociamos la presencia de tensión y a bajo nivel la ausencia de tensión (0) estamos hablando de lo que se llama "lógica positiva".
Si asociamos el nivel bajo o 0 la presencia de tensión y el alto nivel o 1 a la ausencia de tensión, estamos hablando de una "lógica negativa", como se muestra en la figura 24.
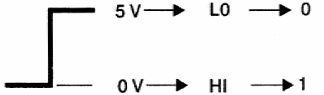
Para no causar ninguna confusión en nuestros lectores, todo nuestro curso se ocupará exclusivamente de la lógica positiva, así como de los dispositivos electrónicos tomados como ejemplo.
Vea entonces que en nuestra lógica podemos asociar los siguientes estados de un circuito con valores 0 y 1:
0 volt
Falso
Apagado
Nivel bajo o LO (*)
(*) De low, “bajo” en inglés.
5 volts (u otra tensión positiva, dependiendo del circuito)
Verdadera
Conectado
Alto nivel o HI (*)
(*) De high, “alto" en inglés.
2.3 - Operaciones Lógicas
En el día a día estamos acostumbrados a realizar varios tipos de operaciones algebraicas, siendo las más comunes las que implican números, es decir, las cantidades que pueden variar o variables. Así que estamos mucho más acostumbrados a trabajar con el Álgebra Clásica.
A partir de esta idea, podemos representar una suma como:
Y = A + B
Donde el valor que encontraremos para Y depende de los valores que vamos a asignar las letras A y B.
Decimos que tenemos en este caso una función algebraica y que el valor de Y es la variable dependiente, porque su valor dependerá precisamente de los valores de A y B son las variables independientes.
En la electrónica digital, sin embargo, hay operaciones más sencillas que la suma, y que pueden ser perfectamente implementadas teniendo en cuenta el uso del Álgebra Booleana.
Es interesante notar que con un pequeño número de estas operaciones podemos llegar a una multitud de operaciones más complejas, por ejemplo, las utilizadas en microprocesadores, microcontroladores y muchos otros circuitos digitales que, repetidos en gran cantidad, o llevado a un grado muy grande de complejidad, nos hacen creer que la máquina sea ¡"inteligente"!
De hecho, es la asociación de una cierta forma de operaciones sencillas que nos lleva al comportamiento muy complejo de muchos circuitos digitales, como se muestra en la figura 25.
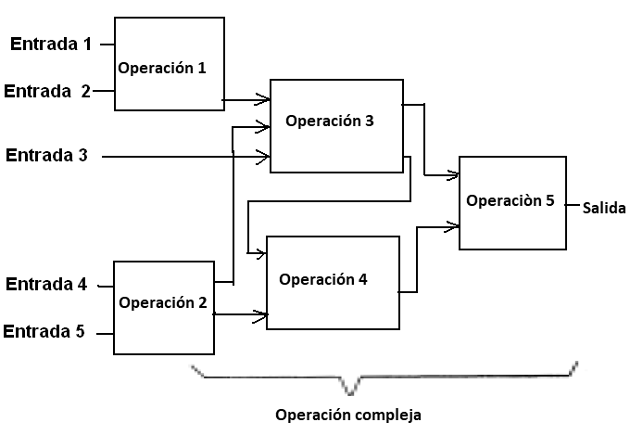
A partir de un ejemplo, podemos tomar un circuito de procesamiento digital que consiste en un gran número de pequeños bloques, llamados puertas o funciones, como se muestra en la figura 26, en el que tenemos entradas y salidas.
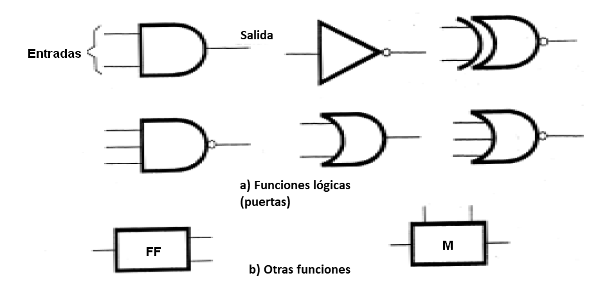
Lo que aparecerá en la salida está determinado por la función y por lo que ocurre en las entradas. En otras palabras, la respuesta que cada circuito lógico, para una entrada o entradas dadas, depende de qué es o qué "regla booleana" que sigue.
Esto significa que para entender cómo funcionan los circuitos digitales desde el más simple hasta el equipo que tiene un microprocesador que realiza las operaciones más complejas, tendremos que empezar por entender cómo el hace que las operaciones más sencillas con las llamadas puertas y lo cuales son.
Por esta razón, después de definir estas operaciones lógicas, asociarlas con el Álgebra Boole, las estudiaremos una a una.
2.3.1 – Razonamiento Lógico y anotaciones
Cuando trabajamos con la electrónica digital, cuando tratamos con el funcionamiento de los circuitos básicos, como lo estamos haciendo aquí, es importante que el lector se familiarice con la jerga utilizada cuando se trata de razonamiento lógico.
Así, las cuestiones relacionadas con el razonamiento lógico están siempre formadas por proposiciones que demuestran, dan razón o apoyan, consistente en afirmaciones que expresan un pensamiento de significado llamado completo.
Estas proposiciones, como hemos visto al tratar con el Álgebra de Boole, tienen, siempre dos posibilidades: pueden tener un sentido positivo o negativo.
Entonces podemos decir:
José enciende una lámpara (sentido positivo)
Mario no utiliza el osciloscopio (sentido negativo)
Los dos ejemplos caracterizan una afirmación o proposición.
A partir de ahí, llegamos a la base de las estructuras lógicas que consisten en saber lo que es verdad o mentira, o utilizando una jerga más adecuada, que es verdad o falsa.
Por lo tanto, existen algunos principios básicos que rigen las proposiciones, cuyos resultados siempre deben ser los mismos.
Principio de contradicción
Ninguna proposición puede ser, al mismo tiempo, falsa y verdad.
Tercero excluido
Dadas dos proposiciones lógicas contradictorias, sólo una de ellas es cierta. Una proposición es verdad o falsa, y no existe un tercer valor lógico. Para la Proposición "él utiliza el osciloscopio" o "él no utiliza el osciloscopio", no hay término medio.
En el estudio de la lógica, y también de la electrónica digital, el uso de las Conjunciones Lógicas es común. Estos son símbolos que se unen desde las proposiciones de uno a otro, o incluso los transforman en una tercera proposición. Las principales Conjunciones Lógicas son:
(~) "No": negación.
(Λ) "E": conjunción.
(V) "o": disyunción.
(→) "Si... Entonces ".
Condicional (↔).
"Si y sólo si": bicondicional.
Todos estos conjunciones se traducirán en funciones lógicas, o circuitos que funcionen siguiendo las leyes de la lógica que veremos a partir de ahora.
Vea que hay una notación para la lógica que es diferente de la utilizada en la electrónica digital y también en las matemáticas. En el estudio de las funciones, a partir de ahora, para facilitar la comprensión de los lectores, incluyendo los que tienen formación en matemáticas, vamos a dar las calificaciones posibles.
La notación matemática proviene de la teoría de los conjuntos. Es la rama de las matemáticas que estudia los conjuntos o colecciones de elementos.
Esta teoría fue inicialmente estudiada por Georg Cantor y Richard Dedekind en 1870 y hoy es adoptada en cursos de matemática en todo el mundo.
La lógica de las clases, que veremos más adelante, puede considerarse como un pequeño fragmento de la teoría de los conjuntos.
En esta lógica tenemos las siguientes anotaciones equivalentes para la lógica y la teoría de los conjuntos:
A ∩ B equivale a a ˄ b. (A intersección B)
A U B equivale a a ˅ b. (A unión B)
A ⸦ B equivale a a → b
a Є P Equivale a p(a)
Ø Equivale a F(FALSO)
U Equivale a V(VERDADERO)
Ā Equivale a ~a
2.4 - Función Lógica NO o Inversora
También encontramos en los manuales la indicación de esta función con la correspondiente palabra inglesa que es NOT.
Lo que esta función hace, es negar una declaración, es decir, cómo en el Álgebra Booleana sólo hay dos posibles respuestas a una pregunta, esta función "invierte" la respuesta, es decir, la respuesta es la "inversa" de la pregunta. El circuito que realiza esta operación se llama inversor.
Si la entrada es "sí" o nivel lógico 1, la salida es "no", o nivel lógico 0.
Teniendo en cuenta entonces que este circuito dice sí, cuando la entrada no es, o que presenta nivel 0, cuando la entrada 1 y viceversa, podemos asociarlo a un tipo de tabla que será de gran utilidad cada vez que estudiemos cualquier tipo de circuito o función lógica.
Esta tabla nos muestra lo que sucede con la salida de la función cuando ponemos en la entrada todas las combinaciones posibles de niveles lógicos.
Decimos que se trata de una "tabla verdad" (en los manuales en inglés esta tabla aparece con el nombre "Truth Table"), y para la puerta NOT o Inversora se muestra a continuación:
Tabla verdad
| 0 | 1 |
| 1 | 0 |
Los símbolos adoptados para representar esta función se muestran en la figura 27.
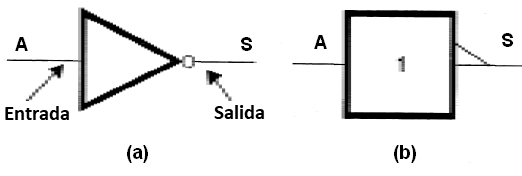
El normalmente adoptado en nuestras publicaciones, y que se usará en este curso, se muestra, pero hay muchos manuales técnicos e incluso diagramas en los que otros son adoptados. Los lectores deben saberlo todo, dada la posibilidad de tener en mano el equipo manual de las más diversas procedencias.
Siendo A la entrada y A la salida podemos escribir la ecuación booleana del inversor como:
S = Ā
Donde:
S es la salida
Ā es la entrada
Esta función puede ser simulada por un simple circuito que el lector puede entender fácilmente y que se muestra en la figura 28.
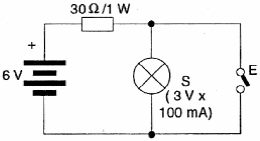
El mismo circuito, utilizando un LED se muestra en la figura 29.
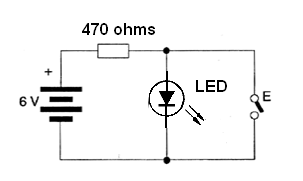
En este circuito tenemos una lámpara, que encendida, indica el nivel 1 en la salida, y apagada, indica el nivel 0 en la salida. Cuando la llave está abierta, indicando que la entrada es nivel 0, la lámpara está encendida indicando que la salida es nivel 1.
Por otro lado, cuando se cierra la llave que representa una entrada 1, la lámpara se borra indicando que la salida es 0.
Esta forma de simular funciones lógicas con lámparas (o LEDs) indicando la salida y las llaves que indican la entrada es ampliamente utilizada en cursos técnicos y para fines didácticos por la facilidad con la que podemos entender su funcionamiento.
Existen otros tipos de circuitos simples que se pueden utilizar para implementar un puerta de propósito didáctico, utilizando relés, transistores y otros componentes fáciles de obtener.
Sólo recuerda eso:
Entrada:
Llave abierta = 0
Llave cerrada = 1
Salida:
Lámpara apagada = 0
Lámpara prendida = 1
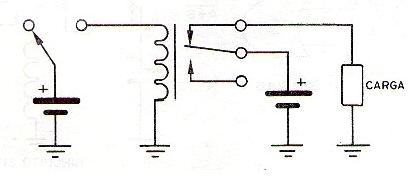
En la figura 30 tenemos un circuito de relé para simular esta función. La carga puede ser un LED de serie con un resistor de 470 ohms o una lámpara y las baterías pueden ser 6 V.
2.5 - Función Lógica E (AND)
La función lógica E, también conocida por su nombre en inglés AND, puede definirse como aquella en la que la salida será 1 sí mismo, y sólo si, todas las variables de entrada son 1.
Vea que en este caso, las funciones lógicas E pueden tener dos, tres, cuatro o tantas entradas como queramos, siendo representado por los símbolos mostrados en la figura 31.
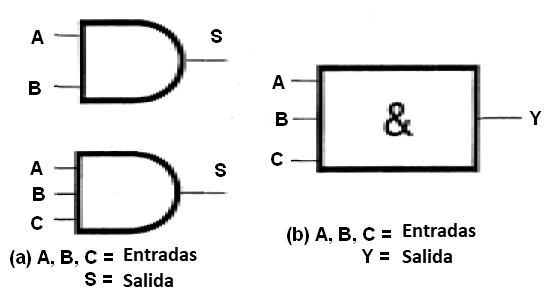
Las funciones lógicas también se denominan "puertas" o "Gates" (del inglés), ya que corresponden a circuitos que pueden controlar o dejar pasar las señales bajo ciertas condiciones.
Tomando como ejemplo una puerta o una función E de dos entradas, podemos escribir la siguiente tabla verdad:
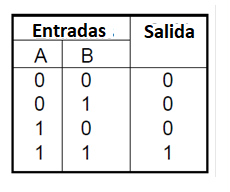
La ecuación Booleana para esta función es:
S = A. B
Donde:
S es la salida
A y B son las entradas
En la figura 32 se muestra cómo simular el circuito de un porto E utilizando llaves y una lámpara común.
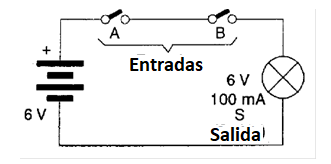
También podemos simular esta función con LED, como se muestra en la figura 33.
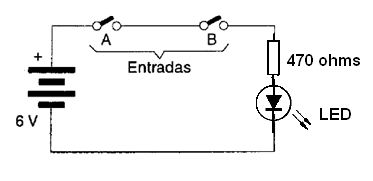
Asegúrese de que los SE y S2 deben estar cerrados de modo que la salida (lámpara o LED) esté activada.
Para una puerta E de tres entradas podemos escribir la siguiente tabla verdad:
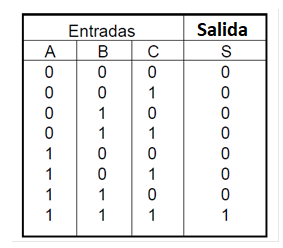
Para que la salida sea 1, todas las entradas deben ser 1.
Vea también el lector que para una puerta E de 2 entradas, tenemos 4 combinaciones posibles para las señales aplicadas. Para una puerta E de 3 entradas, tenemos 8 combinaciones posibles para la señal de entrada.
Para una puerta de 4 entradas, tenemos 16 combinaciones posibles de entradas y así sucesivamente.
2.6 - Función lógica O
La función O, o todavía OR (del inglés), se define como aquella en que la salida está en el nivel alto si una, O más de una de las entradas, está en el alto nivel. Esta función está representada por los símbolos mostrados en la figura 34.
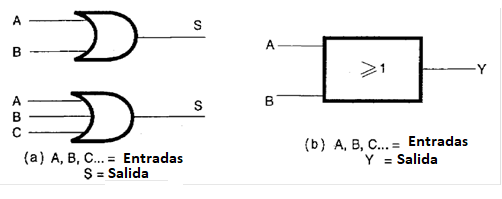
El símbolo normalmente adoptado en nuestras publicaciones se muestra en (a). Sin embargo, hay diagramas y manuales en los que la representación adoptada se muestra en (b).
Para una puerta O de dos entradas podemos elaborar la siguiente tabla verdad:
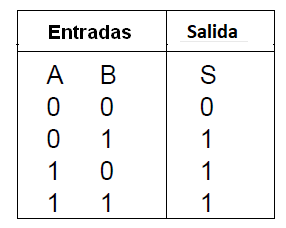
A continuación, vea que la salida estará en el nivel 1 si una O otra entrada estuvieran en el nivel 1.
La ecuación booleana será:
S = A + B
Un circuito sencillo con llaves y lámpara para simular esta función
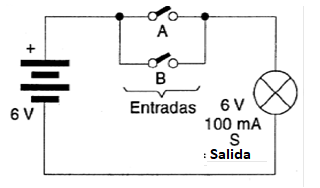
Cuando un O otra llave estuviera cerrada, (entrada 1) la lámpara recibirá corriente (salida 1) como queramos.
También, en este caso, podemos simular la función con otros componentes comunes tales como transistores y relés.
En la figura 36 tenemos un circuito de simulación utilizando LED en lugar de la lámpara indicadora.
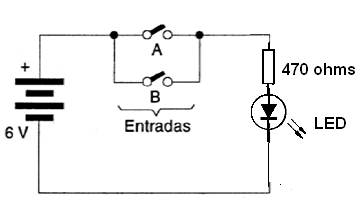
Para más de dos variables podemos tener puertas con más de dos entradas. En el caso de una puerta OU tres entradas, tendremos la siguiente tabla verdad:
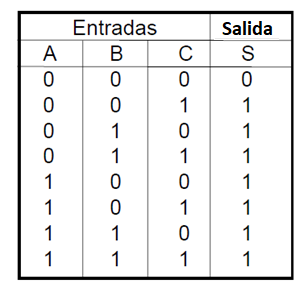
Tenga en cuenta que en esta función tendremos la salida en el nivel inferior con sólo una posible combinación de las entradas: todas las entradas en el nivel bajo.
2.7 - Función NO-Y (NAND)
Las funciones Y, O y No (inversor) son la base de todo el Álgebra Booleana y todos los demás se pueden considerar como derivado de ellos.
Así, una primera función importante, derivada de las anteriores, es la obtenida por la asociación de la función E con la función NO, o sea, la Negación de la función Y que se llama No-Y o del inglés NAND.
En la figura 37 tenemos los símbolos adoptados para representar esta función.
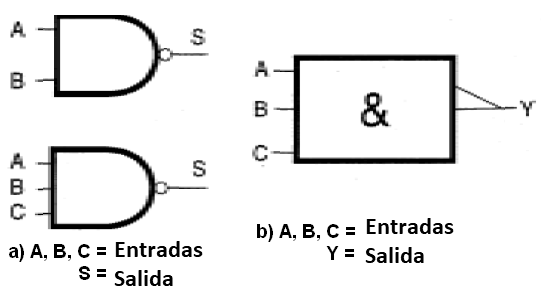
Nótese la existencia de un pequeño círculo a la salida de la puerta para indicar la negación en el caso de la simbología que adoptamos (a). El triángulo en la salida del símbolo que se muestra en (b) indica la negación de la función.
La ecuación booleana para esta función se escribirá como:
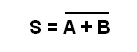
Donde:
S es la salida
A y B son las entradas
El guion sobre la suma indica la negación
Podemos decir que para la función NAND la salida estará en el nivel 0 sí mismo, es sólo si las entradas estuvieran en el nivel 1.
La tabla verdad para una puerta No-E o NAND de dos entradas es como sigue:
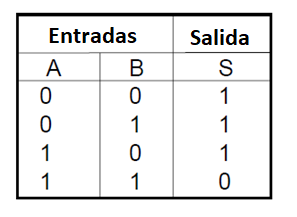
En la figura 37 disponemos de un sencillo circuito con llaves que simulan esta función.
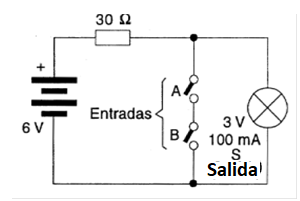
La misma función, simulada con un circuito que usa LED, se muestra en la figura 38.
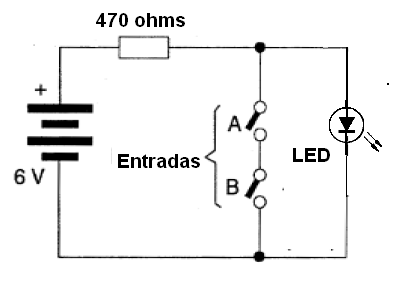
Vea que la lámpara (o LED) sólo se apagara (salida 0) cuando las dos llaves están cerradas (1) cortocircuitando así su alimentación. El resistor se utiliza para limitar la corriente de la fuente.
También en este caso podemos tener la función NAND con más de dos entradas. Para el caso de 3 entradas vamos a tener la siguiente tabla verdad:
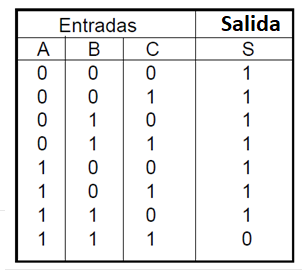
La ecuación booleana para una función NAND o No-E de 3 entradas se escribirá como:
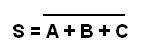
2.8 - Función No-O (NOR)
Esta es la negación de la función O, obtenida por la asociación de la función O con la función No o inversor. El término inglés utilizado para indicar esta función es NOR, y sus símbolos se muestran en la figura 39.
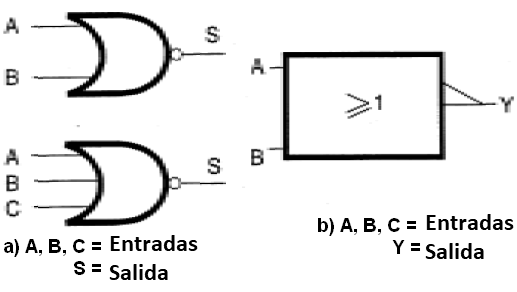
En (a) tenemos la simbología más adoptada en nuestras publicaciones, y en (b) un segundo tipo de simbología que se puede encontrar en muchos manuales técnicos.
Podemos definir su acción de la siguiente manera: la salida será 1 sí mismo, y sólo si, todas las variables de entrada fueran 0.
Una tabla verdad para una función NOR de dos entradas se demuestra abajo:
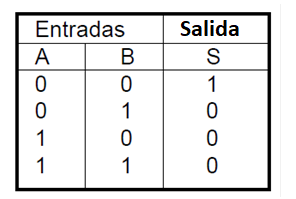
La ecuación booleana para esta función es:
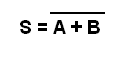
En la figura 40 se muestra un circuito sencillo que utiliza las llaves y la lámpara para simular esta función se muestra en la figura 40.
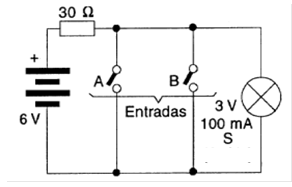
En este caso también podemos elaborar una versión con LED. Como se muestra en la figura 41.
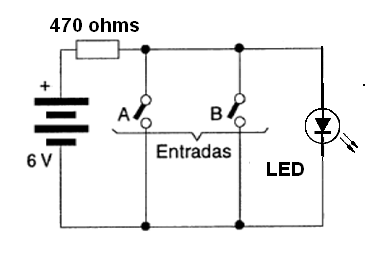
Tenga en cuenta que la lámpara (o LED) sólo permanece encendida (nivel 1) si las dos llaves (S1 y S2) estuvieran abiertas (nivel 0).
Como en los otros ejemplos, podemos implementar esta función experimentalmente utilizando relés, transistores y otros componentes comunes.
De la misma manera que en las funciones anteriores podemos tener puertas NOR con más de dos entradas. Para el caso de tres entradas vamos a tener la siguiente tabla de la verdad:
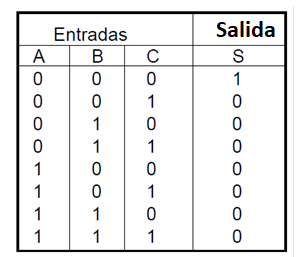
Tenga en cuenta que para esta función todas las salidas estarán en el nivel más alto excepto cuando las tres entradas estén al mismo tiempo en el nivel bajo.
2.9 - Función O-exclusivo (Exclusive-OR)
Una función de gran importancia para el funcionamiento de los circuitos de la lógica digital, y específicamente los que realizan operaciones matemáticas, tales como microprocesadores y microcontroladores, es el llamado O-exclusivo, o usando el término inglés, "Exclusive-OR".
Esta función tiene la propiedad de realizar la suma de valores binarios o aún encontrar lo que se llama "paridad" de los valores binarios, que se verá en el futuro.
En la figura 42 tenemos los símbolos adoptados para esta función.
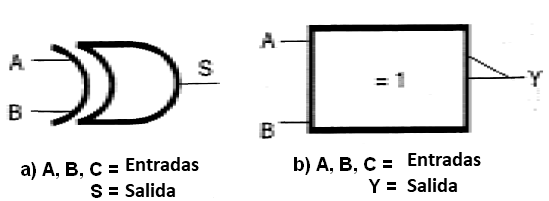
De la misma manera que en casos anteriores, tenemos diferentes simbologías que se pueden encontrar en los manuales y diagramas. El lector debe conocer las dos simbologías, para poder trabajar eficientemente con circuitos digitales.
Podemos definir su acción de la siguiente manera: la salida será 1 sí y sólo si, las variables de entrada serán diferentes. Esto significa que para un puerta Exclusive-OR de dos entradas tendremos salida 1 si las entradas fueran 0 y 1 o 1 y 0, pero la salida será 0 si las entradas son 1 o ambos 0, como se muestra en la siguiente tabla verdad:
La ecuación booleana para esta función es:
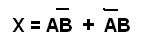
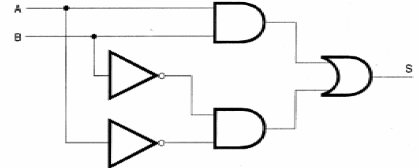
Esta función se deriva de las otras en el sentido de que podemos "montarla" utilizando puertas conocidos, como se muestra en la figura 43.
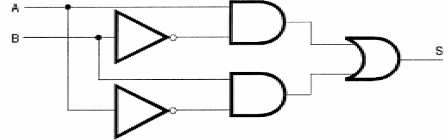
Aunque esta función tiene su propio símbolo, y pueda considerarse un "bloque" independiente en los proyectos, siempre podemos implementarlo con un circuito equivalente como se muestra arriba.
De hecho, como veremos en las lecciones futuras hay varios circuitos integrados que se utilizan en aplicaciones digitales que ya tienen en su interior esta función.
2.10 - Función No-O exclusivo o de coincidencia (Exclusive-NOR)
Podemos considerar esta función como la "inversa" de la O-Exclusivo. Su denominación en inglés es "Exclusive-NOR" representada por el símbolo mostrado en la figura 44.
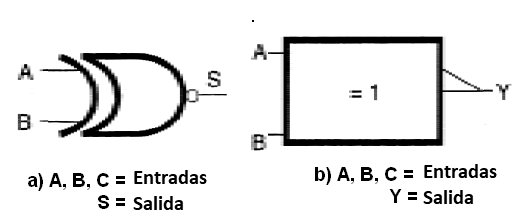
Observe el círculo que indica el negativo de la función anterior, ya que esta terminología no es apropiada en este caso.
En el caso de la simbología mostrada en (b) el triángulo en la salida indica la negación.
Esta función se puede establecer en la que muestra una salida igual a 1 sí y sólo si las variables de entrada fueran las mismas.
Una tabla verdad para esta función es como sigue:
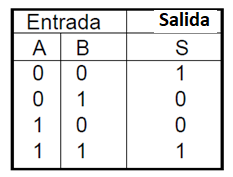
Podemos implementar esta función usando otras ya conocidas como se muestra en la figura 45.
También observamos que podemos encontrar esta función que ya forma parte de muchos circuitos integrados destinados para aplicaciones digitales.
2.11 - Propiedades de las operaciones lógicas
Las puertas realizan operaciones con los valores binarios aplicados a sus entradas.
Así, como hemos visto, podemos representar estas operaciones mediante una simbología adecuada, facilitando así el proyecto de los circuitos y permitiendo una mejor visualización de lo que sucede cuando asociamos muchas funciones.
Sin embargo, para saber asociar los distintos puertas y realizar operaciones más complejas, es necesario conocer las propiedades que las operaciones presentan.
Al igual que en el caso de las operaciones con números decimales, las operaciones lógicas con el álgebra booleana se basan en una serie de postulados y teoremas algo sencillo.
Los principales se dan a continuación y probarlos es a causa de los lectores que desean ir más allá. Para entender, sin embargo, su significado no necesita saber cómo probar su validez, sino más bien memorizar su significado.
Basándonos en las representaciones lógicas que ya hemos estudiado, podemos enumerar las siguientes propiedades de operaciones lógicas:
Estas propiedades se dan en forma de Postulados. Cada profesional que trabajo con circuitos de lógica digital debe saber, por lo tanto, los Postulados de Álgebra Booleana.
a) Leyes de Tautología
"La repetición por suma o multiplicación no cambia el valor real de un elemento."
El circuito mostrado en la figura 46 corresponde a esta ley.
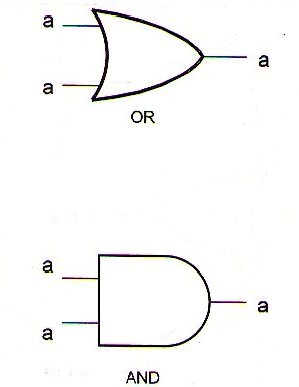
a + a = a
a x a = a
Notación matemática (teoría de los conjuntos)
a ∩ a = a
a U a = a
Notación lógica:
a Λ a = a
a V a = a
b) Leyes de la Conmutación
"La conjunción y la disyunción no se ven afectadas por el cambio secuencial".
La figura 47 muestra los diagramas correspondientes a esta función.
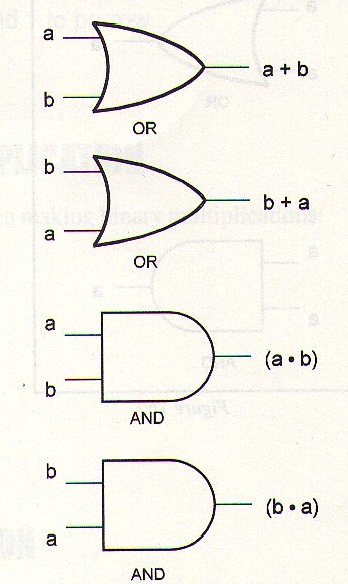
a + b = b + a
a x b = b x a
Notación matemática:
a U b = b U a
a ∩ b = b ∩ a
Notación lógica:
a v b = b v a
a Λ b = b Λ a
c) Leyes de la Asociación
"La agrupación no afecta a la disyunción o conjunciones ".
La figura 48 muestra los circuitos equivalentes.
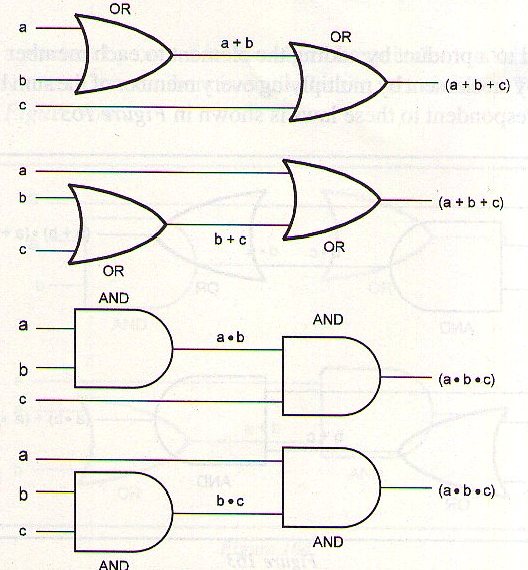
a + (b + c) = (a + b) + c
a x (b x c) = (a x b) x c
Notación matemática:
a U (b U c) = (a U b) U c
a ∩ (b ∩ c) = (a ∩ b) ∩ c
Notación lógica:
a V (b V c) = (a V b) V c
a Λ (b Λ c) = (a Λ b) Λ c
a) Leyes de la Distribución
"Un elemento se agrega a un producto agregando el elemento a cada miembro del producto, y una suma se multiplica por un elemento multiplicando cada elemento de la suma por este elemento.".
El diagrama de circuito equivalente se muestra en la figura 49.
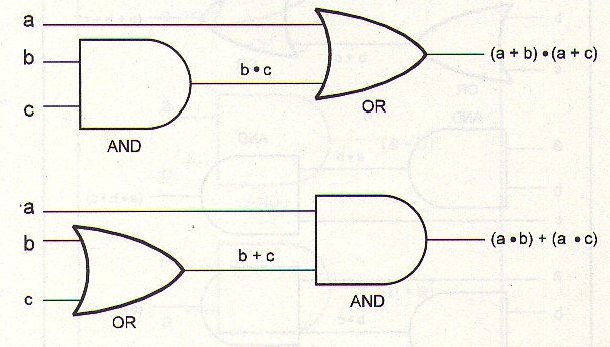
a + (b x c) = (a + b) x (a + c)
a x (b + c) = (a x b) + (a x c)
Notación Matemática:
a U (b ∩ c) = (a U b) ∩ (a U c)
a ∩ (b U c) = (a ∩ b) u (a ∩ a)
Notación Lógica:
a V (b Λ c) = (a V b) Λ (a V c)
a Λ (b V c) = (a Λ b) V (a Λ c)
Leyes de la Absorción
"La disyunción de un producto por parte de uno de sus miembros es equivalente a este miembro. La conjunción de una suma por uno de sus miembros equivale a este miembro ".
El circuito lógico equivalente se muestra en la figura 50.
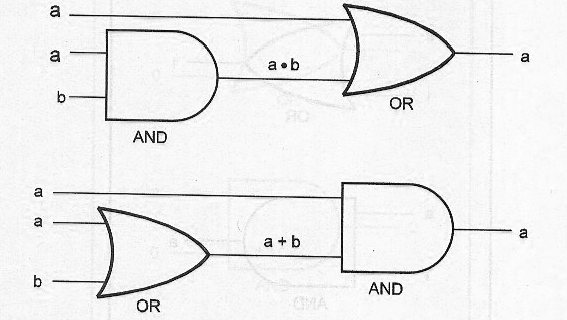
a + (a x b) = a
a x (a + b) = a
Notación matemática:
a U (a ∩ b) = a
a ∩ (a U b) = a
Notación lógica:
a V (a Λ b) = a
a Λ (a V b) = a
Leyes de la Clase Universal
"La suma consistente en un elemento y la clase universal equivale a Clase universal. El producto consistente en un elemento y la clase universal equivale al elemento ".
Los circuitos equivalentes se dan en la figura 51.
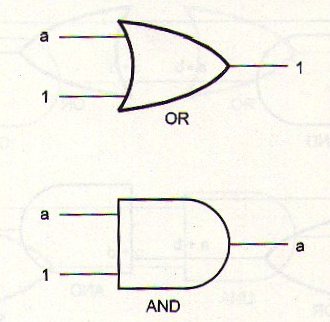
a + 1 = 1
a x 1 = a
Notación matemática:
a U 1 = 1
a ∩ 1 = a
Notación lógica:
a V 1 = 1
a Λ 1 = a
Leyes de la Clase Nula
"La suma consistente en un elemento y la clase Nulo equivale al elemento. El producto que consta de un elemento y la clase Nulo equivale a la clase Nulo ".
Las funciones equivalentes se muestran en la figura 52.
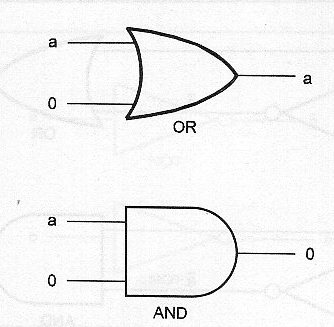
a + 0 = a
a x 0 = 0
Notación matemática:
a U 0 = a
a ∩ 0 = 0
Notación lógica:
a V 0 = a
a Λ 0 = 0
Leyes de Complementación
"La suma consistente en un elemento y su complemento equivale a la clase universal. El producto consistente en un elemento y su complemento equivale a la clase nula ".
En la figura 53 tenemos la representación de estas leyes.
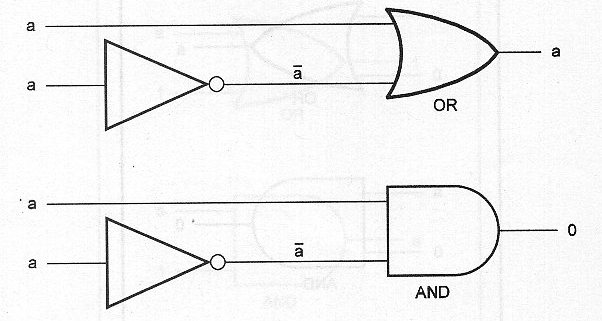
Leyes de contraposición
"Si un elemento a es equivalente al complemento de un elemento b esto implica que el elemento b es equivalente al complemento del elemento a".
La figura 54 representa el diagrama lógico equivalente.
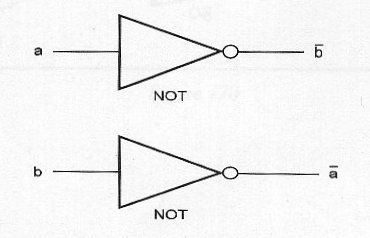
Notación Lógica:
a = /b → b = /a
Notación matemática:
a = b' → b = a'
Ley de Negación Doble
“El complemento de la negación de un elemento es equivalente al elemento".
La figura 55 muestra el circuito lógico equivalente.
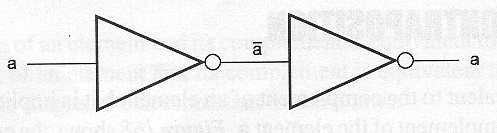
Notación matemática:
a = a'C
Notación lógica:
a =-a '
Leyes de Expansión
"La disyunción de un producto consistente en los elementos a y b y un producto compuesto del elemento a y elemento de elemento de complemento b es equivalente al elemento a. La conjunción de una suma compuesta por los elementos a y b y la suma compuesta del elemento a y complementar el elemento b es equivalente al elemento a.
La figura 56 muestra los circuitos lógicos equivalentes.
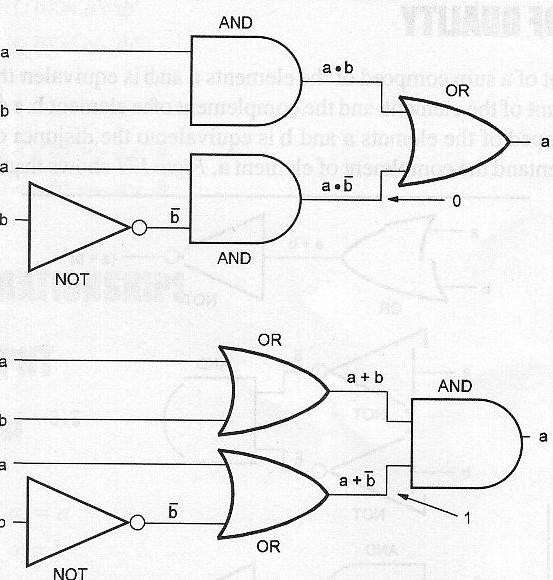
Notación matemática:
(a ∩ b) U (a ∩ b') = a
(a U b) ∩ (a U b') = a
Notación lógica:
(a Λ b) V (a Λ ~b) = a
(a V b) Λ (a V ~b) = a
Leyes de la Dualidad
"El complemento de una suma compuesta por los elementos a y b es equivalente a la conjunción del complemento de la a y el complementar el elemento b. El complemento de un producto consistente en los elementos a y b equivale a la disyunción del complemento de la a y complementar el elemento a”.
En la figura 57 tenemos los circuitos lógicos equivalentes.
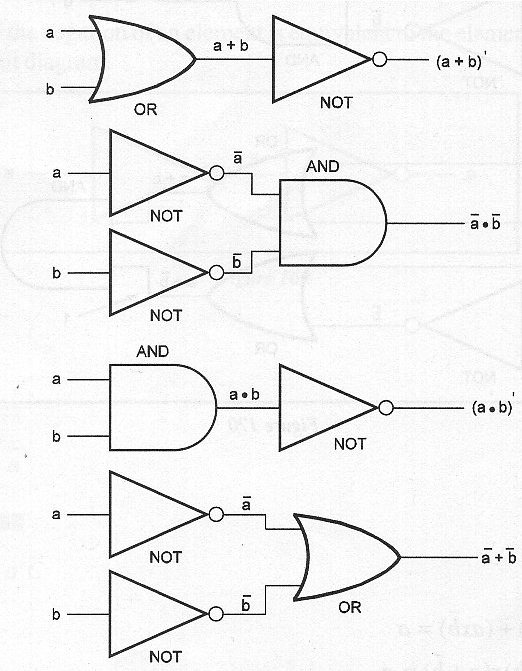
Notación matemática
(a U b)' = a' ∩ b'
(a ∩ b)' = a' U b'
Notación lógica:
~(a V b) = ~a Λ ~b
~(a Λ b) = ~a V ~b
Relaciones Booleana
Aquí hay algunas relaciones importantes que el lector debe memorizar.
Punto de identidad
Adición:
a + 0 = a
a + 1 = 1
a + a = a
Multiplicación
0 x a = 0
1 x a = a
a x a = a
Conmutativa
Adición:
(a + b) = (b + a)
Multiplicación:
a x b = b x a
Asociativa
Adición:
(a + b) + c = a + (b + c)
Multiplicación
(a x b) x c = a x (b x c)
Distributiva
a + (b x c) = a x (b + c)
a + b x c = (a + b) x (a + c)
Absorción
a x (a + b) = a + a x b = a
Teoremas de Morgan:
"Aplicando la operación NO a una operación E, el resultado obtenido es igual al de la operación OU aplicado a los complementos de las variables de entrada ".
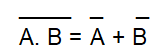
"La aplicación de la operación No a una operación OU el resultado es igual a la operación E aplicada a los complementos de las variables de entrada ".
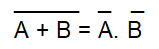
2.12 - Haciendo todo con las puertas NAND o No-Y
Las puertas No-Y, por sus características, se pueden utilizar para obtener cualquier otra función que estudiemos. Esta propiedad hace que estos puertas bloques universales en los proyectos de circuitos digitales ya que, en forma de circuitos integrados, las funciones NAND son fáciles de obtener y también económicas.
A continuación, mostraremos cómo podemos obtener las funciones estudiadas simplemente utilizando puertas NAND.
* Inversor
Para obtener un inversor de un puerta NAND, simplemente unir a sus entradas o colocar una de las entradas en el nivel lógico 1, como se muestra en la figura 58.
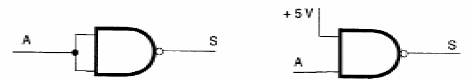
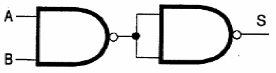
* Se obtiene una puerta Y (AND) simplemente añadiendo a la función No-Y (NAND) un inversor en cada entrada, como se muestra en la figura 59.
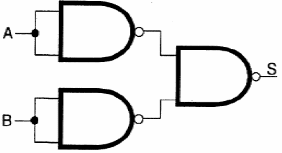
* La función OU puede obtenerse con el circuito mostrado en la figura 60.
Lo que se hace es invertir la salida después de aplicarla a una puerta NAND.
Sumário
Curso de Electrónica - Electrónica Digital (CUR5000)
Curso de Electrónica - Electrónica Digital – Parte 1 (CUR5001S)
Curso de Electrónica Digital – Parte 2 - El Álgebra de Boole (CUR5002S)
Curso de Electrónica - Electrónica Digital - Parte 6 - Los Elementos Biestables (CUR5006S)
Curso de Electrónica - Electrónica Digital - Parte 9 - Contadores Digitales (CUR6002S)
Curso de Electrónica - Electrónica Digital - Parte 13 - Memorias, ADCs y DACs (CUR6006S)




